Ta dùng bơm có diện tích pittong 8 cm2,khoảng chạy 25cm,để bơm một bánh xe đạp sao cho khi áp lực của bánh lên đường là 350N thì diện tích tiếp xúc là 50 cm2.Ban đầu bánh chứa khí ở áp suất khí quyển p0=105Pa và có thể tích V0=1500cm3.Giả thiết sau khi bơm thì diện tích của bánh xe là 2000cm3,và vì ta bơm chậm nên nhiệt độ không đổi.Tính số lần phải bơm?Đáp án:(10 lần)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = F/S = 350/0,005 = 0,7.105 Pa;
→ p = 1,7.105 Pa lớn hơn 1,5p0 nên thể tích sau khi bơm là 2000 cm3.
Mỗi lần bơm có 8.25 = 200 cm3 không khí ở áp suất p0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p1 = p0; V1 = (1500 + 200n)
Trạng thái 2: p2 = 1,7.105 Pa; V2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n c m 3 không khí được đưa vào bánh. Ban đầu có 1500 c m 3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa ; V 2 = 2000 c m 3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần.

Chọn C.
Áp suất trong bánh xe khi bơm xong: p = p 0 + p’
Với p’ = F/S = 350/0,005 = 0,7. 10 5 Pa;
→ p = 1,7. 10 5 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3 .
Mỗi lần bơm có 8.25 = 200 c m 3 không khí ở áp suất p 0 được đưa vào bánh xe. Sau n lần bơm có 200n cm3 không khí được đưa vào bánh. Ban đầu có 1500 cm3 không khí ở áp suất p 0 trong bánh xe. Như vậy có thể coi:
Trạng thái 1: p 1 = p 0 ; V 1 = (1500 + 200n)
Trạng thái 2: p 2 = 1,7. 10 5 Pa; V 2 = 2000 cm3
Áp dụng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tìm được n = 19/2 ≈ 10 lần

Áp suất trong bánh xe khi bơm xong: p = p0 + p’
Với p’ = 350/0,005= 0,7. 10 5 Pa; p = 1,7.105 Pa lớn hơn 1,5 p 0 nên thể tích sau khi bơm là 2000 c m 3
n’ = 2n = 19 lần.

V0 thể tích mỗi lần bơm, p0 là áp suất khí quyển, V là thể tích săm xe ,trọng lượng phần xe đạp tác dụng lên bánh xe đang bơm là F, Ta có: F = p 1 .60 = p 2 . S
Với p1 và p2 là áp suất đầu và sau khi bơm tiêm, S là diện tích tiếp xúc sau khi bơm thêm 20 lần. Vậy S = 60. p 1 p 2 (1)
Theo định luật Bôi lơ – Ma ri ốt
{ 30 v 0 p 0 = v p 1 50 v 0 p 0 = v p 2 ⇒ 30 50 = p 1 p 2 = 3 5 ( 2 )
Thay (2) vào (1) ta có
S = 3 5 60 = 36 c m 2

Đáp án D
- Gọi n là số lần bơm để đưa không khí vào ruột xe.
Vậy thể tích không khí cần đưa vào ruột xe là V1 = nV0 = 80tn cm3.
Và áp suất p1 = l atm.
Áp suất p2 sau khi bơm là
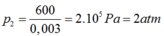
và thể tích V2 = 2000 cm3
Vì quá trình bơm là đẳng nhiệt nên: p1V1 = p2.V2 ó 80n = 2000.2 => n = 50
Vậy số lần cần bơm là 50 lần.
