Trên mặt nước, hai nguồn kết hợp được đặt tại hai điểm O1 và O2 cách nhau 196cm, dao động điều hòa, cùng pha, cùng tần số theo phương vuông góc với mặt nước. Trên cả mặt chất lỏng người ta thấy hai điểm bất động gần nhau nhất cách nhau 10cm. Điểm m là một vị trí cân bằng của phần tử ở mặt nước thuộc đường tròn tâm O1 bán kính O1O2. Phần tử ở M dao động với biên độ cực đại. Khoảng cách O2M lớn nhất bằng?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Bước sóng: λ = v f = 30 10 = 3 c m
Số vân cực đại và cực tiểu thỏa mãn:
− S 1 S 2 λ < k < S 1 S 2 λ − S 1 S 2 λ − 1 2 < k < S 1 S 2 λ − 1 2 ⇒ − 8 3 < k < 8 3 − 8 3 − 1 2 < k < 8 3 − 1 2 ⇒ − 2 , 6 < k < 2 , 6 − 3 , 17 < k < 2 , 17
Như vậy có 5 vân cực đại và 6 vân cực tiểu.

Đáp án D
Ta có:
![]()
Tại P là cực đại:
![]()
![]()
Số cực tiểu trên O 1 P thỏa mãn:
![]()
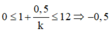

Đáp án D
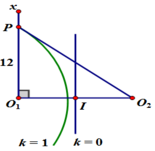
P thuộc O 1 x và xa O 1 nhất => P thuộc đường cực đại k = 1 .
Có
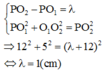
Số đường cực tiểu trên O 1 O 2 :
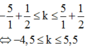
=> có 10 điểm=> trên nửa đoạn thẳng có 5 điểm. Để ý mỗi đường cực tiểu qua điểm cực tiểu trên I O 1 đều cắt PO1 trừ đường giữa k = 0 v à k = 1 . Vì thế trên PO1 có 4 điểm cực tiểu.

Đáp án A
Bước sóng: 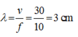
Số vân cực đại và cực tiểu thỏa mãn:
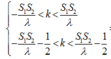
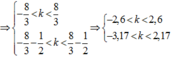
Như vậy có 5 vân cực đại và 6 vân cực tiểu.

Đáp án D
+ Cực đại giao thoa có hiệu đường đi k λ , k = 0 ; ± 1 ; ± 2 ; . . .

Đáp án D
+ Cực đại giao thoa có hiệu đường đi ∆ d = k λ với k = 0 , ± 1 , ± 2 . . .

Đáp án: B
HD Giải: λ/2 = 10mm => λ = 20mm

BC lớn nhất khi C nằm trên cực đại số 3 và gần A nhất
Ta có 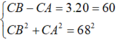
=> CB = 67,6mm


Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D
À, mình làm nhầm, vị trí vân cực đại này phải là: \([\dfrac{196}{20}]=9\)
\(\Rightarrow d_2-d_1=9.\lambda=9.20=180cm\)
\(\Rightarrow d_2=376cm\)