Từ một điểm S ở ngoài đt (o) kẻ tiếp tuyến SA và một các tuyến SBC ( góc BAC <90) Phân giác góc BAC cắt BC tại D và cắt đt tại điểm thứ hai là E Cac tiếp tuyến của đt (o) tại C và E cắt nhau tại N. P là giao điểm AE và CNCM a ) SA =SD B) EN//BC C) \(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\) ANH CHỊ GIÚP E VỚI Ạ CÂU C Í Ở MATHONLINE KHÔNG AI GIÚP EM MỚI SANG...
Đọc tiếp
Từ một điểm S ở ngoài đt (o) kẻ tiếp tuyến SA và một các tuyến SBC ( góc BAC <90) Phân giác góc BAC cắt BC tại D và cắt đt tại điểm thứ hai là E Cac tiếp tuyến của đt (o) tại C và E cắt nhau tại N. P là giao điểm AE và CN
CM a ) SA =SD B) EN//BC C) \(\frac{1}{CN}=\frac{1}{CD}+\frac{1}{CP}\) ANH CHỊ GIÚP E VỚI Ạ CÂU C Í Ở MATHONLINE KHÔNG AI GIÚP EM MỚI SANG ĐÂY
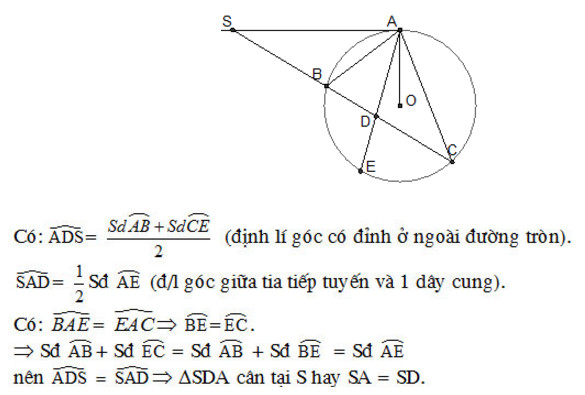
a, Do AE là phân giác CAB nên CAD = DAB (1)
mà SA là tiếp tuyến của đường tròn nên SAB = ACB (do cùng chắn cung AB) (2)
từ (1) và (2) ta có CAD + ACB = DAB + SAB = DAS
mà ADB = CAD + ACB (do ADB là góc ngoài tam giác ACD)
=> DAS = ADB => tam giác SAD cân => SA = SD
b, ta có AEx = ACE ( do cùng chắn cung AE)
mà ACE = SAE ( do cùng chắn cung AE)
=> AEx = SAE mà SAE = SDA (tam giác cân)
=> AEx = SDA mà SDA = CDE (đđ) và AEx = NEP(đđ)
NEP = CDE mà ở vị trí đồng vị => BC // EN
c, tam giác PCD có NE // CD => \(\frac{NE}{CD}\)= \(\frac{NP}{CP}\)
=> NE x CP = CD x NP
mà NE = CN (t/c tiếp tuyến cắt nhau); NP = CP - CN
=> CN x CP = CD x CP - CD x CN
=> CN( CP + CD) = CD x CP
=>\(\frac{1}{CN}\)= \(\frac{CP+CD}{CDCP}\)
=> \(\frac{1}{CN}\)= \(\frac{1}{CP}\)+\(\frac{1}{CD}\)