Tìm tọa độ điểm M trên đồ thị (C) của hàm số \(y=x^3-3x+2\) sao cho tiếp tuyến với (C) tại M cắt (C) tại N sao cho \(MN=2\sqrt{6}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Ta có: ![]()
Suy ra PTTT của (C) tại M là ![]()
Khi đó PT hoành độ giao điểm của (C) và ![]() là:
là: ![]()

Đáp án C
Phương trình tiếp tuyến của (C) tại M k x k ; y k là y = y k = y ' x k x - x k
⇔ y = y ' x k x - x k + y k = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ( d )
Phương trình hoành độ giao điểm của (C) và tiếp tuyến (d) là
x 3 - 2018 x = 3 x k 2 - 2018 x - x k + x k 3 - 2018 x k ⇔ x - x k x 2 + x k x - 2 x k 2 = 0 ⇔ [ x = x k x = - 2 x k Do đó x k + 1 = - 2 x k suy ra x 1 = 1 ; x 2 = - 2 ; x 3 = 4 ; . . . ; x n = ( - 2 ) n - 1 ( cấp số nhân với q = -2)
Vậy 2018 x n + y n + 2 2019 = 0 ⇔ x n 3 = - 2 2019 ⇔ - 2 3 n - 3 = - 2 2019 ⇒ n = 674

Gọi k là hệ số góc của tiếp tuyến tại M, N thì \(x_M;x_N\) là nghiệm của phương trình :
\(f'\left(x\right)=k\Leftrightarrow3x^2-6x-k=0\)
Để tồn tại hai tiếp điểm M, N thì phải có \(\Delta'>0\Leftrightarrow k>-3\)
Ta có \(y=f'\left(x\right)\left(\frac{1}{3}x-\frac{1}{3}\right)-2x+2\)
Từ \(f'\left(x_M\right)=f'\left(x_N\right)=k\) suy ra phương trình đường thẳng MN là :
\(y=\left(\frac{k}{3}-2\right)x+2-\frac{k}{3}\), khi đó \(A\left(1;0\right);B\left(0;\frac{6-k}{3}\right)\)
Ta có \(AB^2=10\Leftrightarrow k=15\) (do k > -3)
Từ đó ta có 2 tiếp tuyến cần tìm là :
\(y=15x-12\sqrt{6}-15\)
\(y=15x+12\sqrt{6}-15\)

- Tiếp tuyến (d) tại điểm M của đồ thị (C) có hoành độ x 0 = 0 ⇒ y 0 = 3 .
- Ta có:
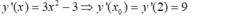
- Phương trình tiếp tuyến (d) tại điểm M của đồ thị (C) là:
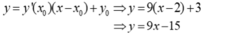
- Xét phương trình hoành độ giao điểm của đồ thị (C) và đường thẳng d là nghiệm phương trình :
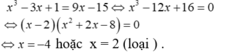
- Với x = -4 thì y = 9.(-4) – 15 = -51.
- Vậy N(- 4 ; -51) là điểm cần tìm.
Chọn C.

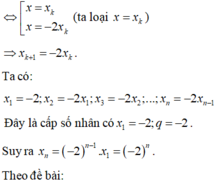

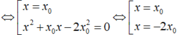
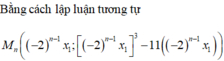

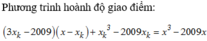
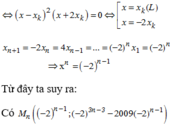
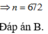
Gọi \(M\left(x_0;x^3_0-3x_0+2\right)\) là tiếp điểm. Phương trình tiếp tuyến là :
\(\Delta:y=\left(3x^2_0-3\right)\left(x-x_0\right)+x^3_0-3x_0+2\)
Giả sử \(N\left(a;a^3-3a+2\right)\in\left(C\right),\left(a\ne x_0\right)\)
Tiếp tuyến \(\Delta\) đi qua N nên :
\(a^3-3a+2=\left(3x^2_0-3\right)\left(a-x_0\right)+x_0^3-3x_0+2\)
\(\Leftrightarrow\left(a-x_0\right)^2\left(a+2x_0\right)=0\Leftrightarrow a=-2x_0;\left(x_0\ne a\right)\)
Suy ra \(N\left(-2x_0;-8x_0^3+6x_0+2\right)\)
Ta có \(MN=2\sqrt{6}\Leftrightarrow9x^2_0+\left(9x_0^3-9x_0\right)^2=24\Leftrightarrow x^2_0=\frac{4}{3}\)
Ta được 2 điểm là \(M\left(\frac{2\sqrt{3}}{3};\frac{10\sqrt{3}}{9}+2\right):M\left(-\frac{2\sqrt{3}}{3};\frac{10\sqrt{3}}{9}+2\right)\)