Cho đường thẳng d: 2x - y + 10 =0 và điểm M(1; -3)
a) Tính khoảng cách từ điểm M đến đường thẳng d
b) Viết pt đường thẳng đi qua M và vuông góc với đường thẳng d
c) Viết pt tiếp tuyến với đường tròn (C): (x-2)2 + (y-3)2 =9 biết rằng tiếp tuyến đó song song với đường thẳng d
d) Cho ∆ABC biết tọa độ trực tâm H(2;2). Tâm đường tròn ngoại tiếp ∆ABC là điểm I(1;2). Xác định tọa độ các điểm A, B, C biết trung điểm của BC là điểm M(1;1) và hoành độ điểm B âm

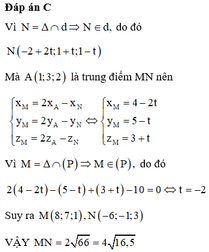

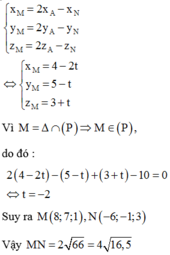
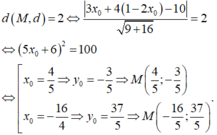
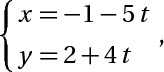 d2:
d2: 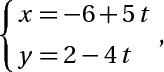
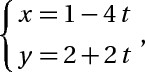 d2 : 2x+4y-10=0
d2 : 2x+4y-10=0
Giúp mik câu d với