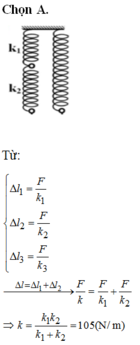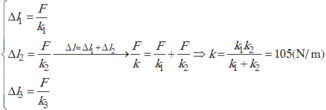Một lò xò có hệ số đàn hồi k= 20 N/m, người ta kéo lò xò dãn 10cm. Khi thả lò xò từ độ dãn 10cm cuống 4cm, lực đàn hồi của lò xo sinh ra một công:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tóm tắt: \(k=100\)N/m;\(\Delta l=4cm=0,04m\)
\(F_{đh}=?\)
Bài giải:
Độ lớn lực đàn hồi:
\(F_{đh}=k\cdot\Delta l=100\cdot0,04=4N\)

Áp dụng độ biến thiên thế năng
A = W t 1 − W t 2 = 1 2 k ( x 1 2 − x 2 2 ) = 1 2 .100 ( 0 , 02 2 − 0 , 04 2 ) = − 0 , 06 ( J )

a) Độ lớn của lực đàn hồi:
![]()
b) Thế năng đàn hồi:
![]()
c) Công thực hiện của lò xo:
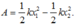
thay số:
![]()
Công A<0 vì lực đàn hồi ngược với chiều biến dạng, công của lực đàn hồi là công cản.

a)Độ lớn của lực đàn hồi: \(F_{đh}=5N\)
b)Độ biến dạng của lò xo: \(\Delta l=\dfrac{F_{đh}}{k}=\dfrac{5}{100}=0,05m=5cm\)
c)Để lò xo dãn thêm 2cm tức \(\Delta l'=2+5=7cm=0,07m\)
Lực đàn hồi lúc này: \(F'_{đh}=0,07\cdot100=7N\)
Cần tăng lực kéo thêm: \(\Delta F=7-5=2N\)

\(\Delta l=4cm=0,04m\)
a)Độ cứng lò xo:
\(k=\dfrac{F}{\Delta l}=\dfrac{10}{0,04}=250\)N/m
b)Thế năng đàn hồi của lò xo bị nén lại 6cm:
\(W_t=\dfrac{1}{2}kx^2=\dfrac{1}{2}\cdot250\cdot0,06^2=0,45J\)
c)Độ biến thiên thế năng đàn hồi:
\(A=W_{đh1}-W_{đh2}=\dfrac{1}{2}kx'^2-0,45\)
\(=\dfrac{1}{2}\cdot250\cdot0,03^2-0,45=-0,3375J\)
Công này có tác dụng chống lại sự biến dạng.