Xác định nhiệt cân bằng nhiệt và biến thiên entropy khi trộn 1g nước ở 0 độ C và 10g nước ở 100 độ C. Cho biết nhiệt nóng chảy của đá bằng 334,4 J/g và nhiệt dung diêng của nước bằng 4,18 J/g.k
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình cân bằng nhiệt:
lmth + cthmth(t2 – t) = cnmn(t – t1) + Cnlk(t – t1)
ð l = c n m n ( t − t 1 ) + C n l k ( t − t 1 ) − c t h m t h ( t 2 − t ) m t h = 60 J/g.

Đáp án: A
Phương trình cân bằng nhiệt:
Qthu = Qtỏa
cnmn(t – t2) + Cnlk(t – t2)
= lmth + cthmth(t1 – t)
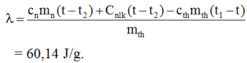

Nhiệt lượng cần phải cung cấp để làm cho một cục nước đá có khối lượng 200 g nước đá ở -20 ° C tan thành nước và được đun sôi để biến hoàn toàn thành hơi nước ở 100 ° C
Q = c đ m( t 1 - t 0 ) + λ m + c n m( t 2 - t 1 ) + Lm
hay Q = m [ c đ ( t 1 - t 0 ) + λ + c n ( t 2 - t 1 ) + L]
Thay số, ta tìm được :
Q = 0,2. [2,09. 10 3 (0 - (-20)) + 3,4. 10 5 + 4,18. 10 3 (100 - 0) + 2,3. 10 6 ]
hay Q = 205 960 J ≈ 206 kJ

Đáp án: B
Phương trình cân bằng nhiệt:
cm2(t2 – t) = lm1 + cm1t
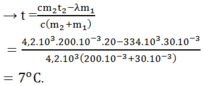

Phương trình cân bằng nhiệt:
c m 2 ( t 2 - t ) = λ m 1 + c m 1 t ð t = c m 2 t 2 − λ m 1 c ( m 2 + m 1 ) = 7 ° C
Gọi T (K) là nhiệt độ của hệ sau khi trộn. Giả sử hệ là cô lập.
Ta có phương trình:
Nhiệt lượng tỏa ra = Nhiệt lượng thu vào
\(Q_{tỏa}=Q_{thu}\) hay \(Q_3=Q_1+Q_2\)
\(\Leftrightarrow\) - 10.4,18.(T - 373) = 334,4 + 1.4,18.(T - 273)
- 10.4,18.(T - 373) = 334,4 + 1.4,18.(T - 273)
\(\Rightarrow\) T = 356,64 (K)
T = 356,64 (K)
\(\begin{matrix}1gH_2O\left(r\right)\\273k\end{matrix}\)------------->\(\begin{matrix}1gH_2O\left(l\right)\\273k\end{matrix}\)---------------->\(\begin{matrix}1gH_2O\left(l\right)\\T\left(K\right)\end{matrix}\)<-----------------\(\begin{matrix}10gH_2O\left(l\right)\\373k\end{matrix}\)
\(\Delta S_1\) \(\Delta S_2\) \(\Delta S_3\)
\(\Delta S=\Delta S_1+\Delta S_2+\Delta S_3\)
Với: \(\Delta S_1=\frac{\lambda_{nc}}{T_{nc}}=\frac{334,4}{273}=1,225\left(J\text{/}K\right)\)
\(\Delta S_1=\frac{\lambda_{nc}}{T_{nc}}=\frac{334,4}{273}=1,225\left(J\text{/}K\right)\)
\(\Delta S_2=1.\int\limits^{356,64}_{273}4,18.\frac{dT}{T}=1,117\left(J\text{/}K\right)\)
\(\Delta S_3=10.\int\limits^{356,64}_{373}4,18\frac{dT}{T}=-1,875\left(J\text{/}K\right)\)