Tính tổng của n số hạng \(T_n=105+110+115+....+995\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
15 tháng 6 2021
Mỗi số hạng (kể từ số hạng thứ 2) bằng số hạng đứng trước nó cộng với một số tự nhiên 2.
a, Số số hạng = (Số hạng cuối - Số hạng đầu ) : khoảng cách + 1
115 = (a-101) :2 +1
a-101= (115-1) x 2
a= 228-101= 127
Vậy số hạng thứ 115 của dãy số đã cho là 127
b, Tổng của dãy= (Số hạng lớn nhất của dãy + số hạng bé nhất của dãy) x số số hạng có trong dãy : 2
=(127+101) x 115 : 2
=13110
VN
27 tháng 4 2017
Đổi: 105% = 21/20; 110% = 11/10
B = 105%.A => B = \(\frac{21}{20}.A\)
C = 110%.B => C = \(\frac{11}{10}.B\)
\(\Rightarrow C=\frac{11}{10}.\frac{21}{20}A\)
\(\Rightarrow C=\frac{231}{200}A\)
Tổng 3 số là: \(A+B+C=A+\frac{21}{20}A+\frac{231}{200}A=\frac{641}{200}A\)
PS: Hoang mang quá =))
BN
2
4 tháng 6 2015
dãy là :102+105+108+111+114+117+120+123+126+129
Số các số hạng là :
(129 -102 ) : 3 + 1 = 10 (số )
Tổng của dãy là :
(129 + 102 ) x10 : 2=1155
theo công thức lớp 6 đ ú n g mình nha
DN
4 tháng 6 2015
Mih nhầm
102+105+108+111+114+117+120+123+126+129
Số phần tử của dãy trên là:
(129-102):3+1=10(phần tử)
Tổng:
(129+102).10:2=1155
**** mình nha
4 tháng 12 2023
a:
\(0< =cos\left(\dfrac{\Omega}{2n}\right)< =1;n\in Z^+\)
Khi n chẵn thì \(\left(-1\right)^n=1\)
=>\(u_n=cos\left(\dfrac{\Omega}{2n}\right)\)
=>\(0< =u_n< =1\)
=>\(\left(u_n\right)\) bị chặn ở khoảng [0;1]
Khi n lẻ thì \(\left(-1\right)^n=-1\)
=>\(u_n=-cos\left(\dfrac{\Omega}{2n}\right)\)
\(0< =cos\left(\dfrac{\Omega}{2n}\right)< =1\)
=>\(0>=-cos\left(\dfrac{\Omega}{2n}\right)>=-1\)
=>\(0>=u_n>=-1\)
=>\(\left(u_n\right)\) bị chặn ở khoảng [-1;0]
b: \(-1< =\dfrac{1}{5^n}< =0\)
=>\(-\sqrt{2}< =\dfrac{\sqrt{2}}{5^n}< =0\)
=>\(-\sqrt{2}< =t_n< =0\)
Vậy: Dãy số bị chặn ở khoảng \(\left[-\sqrt{2};0\right]\)
3 tháng 3 2020
105 105 105 105 105 105 105 105 110 110 110 110
115 115 115 115 115 115 120 120 120 120 120 120
125 125 125 125 130 130
Ko kẻ bảng đc! Sorry nha!
Chúc bạn học tốt!
CM
20 tháng 9 2018
C=3-1+4-1+5-1+....+102-1+103-1
C=2+3+4+5+...+101+102
Tổng đã cho có: (102-2):1+1=101 (số hạng)
C=(102+2)*101:2=5252
Vậy 5252 là tổng của tập hợp C.
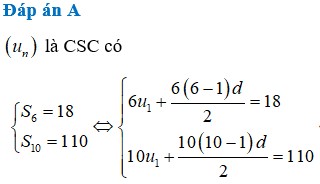
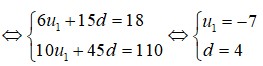
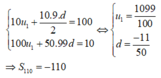
Xét cấp số cộng (U\(_n\)) có u\(_1\)=105 và công sai d =5 ta đươc:
995=u\(_n\)=u\(_1\)+(n-1)d =105+5(n-1)\(\Leftrightarrow\)n=179
s=s\(_{179}\)=\(\frac{179}{2}\)(u\(_1\)+u\(_{179}\))=\(\frac{179}{2}\)(105+995)=98450
Ta có : \(a_1=105;a_2=110\Rightarrow d=5;a_n=995\)
mà \(a_n=a_1+\left(n-1\right)d\Rightarrow995=105+\left(n-1\right)5\)
\(\Rightarrow S=\frac{n\left(a_1+a_n\right)}{2}=98450\)