Cho hình chóp SABC có tam giác ABC vuông tại A, AB=AC=a. I là trung điểm của SC.Hình chiếu vuông góc của S lên mp (ABC) là trung điểm H của BC , mp (SAB) tạo với đáy một góc 60. Tính thể tích khối chóp SABC và khoảng cách từ I tới mp (SAB) theo a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


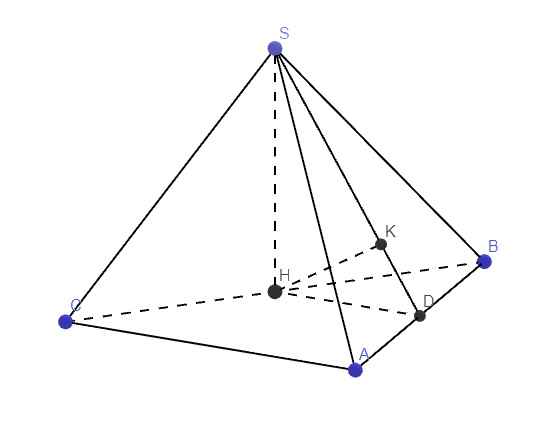
Gọi D là trung điểm AB \(\Rightarrow HD\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}HD||AC\Rightarrow HD\perp AB\\HD=\dfrac{1}{2}AC=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow AB\perp\left(SHD\right)\)
\(\Rightarrow\widehat{SDH}\) là góc giữa (SAB) và đáy
\(\Rightarrow\widehat{SDH}=60^0\)
\(\Rightarrow SH=DH.tan60^0=\dfrac{a\sqrt{3}}{2}\)
Từ H kẻ \(HK\perp SD\) (K thuộc SD)
\(\Rightarrow HK\perp\left(SAB\right)\Rightarrow HK=d\left(H;\left(SAB\right)\right)\)
\(HK=\dfrac{SH.DH}{\sqrt{SH^2+DH^2}}=\dfrac{a\sqrt{3}}{4}\)

Chọn B
ta có: d ( I , ( S A B ) ) = 1 2 d ( C , ( S A B ) )
lại có: d ( C , ( S A B ) ) = 3 V S A B C S Δ A B C
gọi M là trung điểm AB, khi đó góc giữa mp(SAB) và mp(ABC) là góc S M H ^
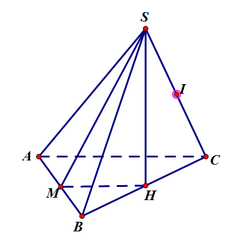
khi đó: S H = H M . tan 60 o = a 3 2
V S A B C = a 3 3 12 ; S A B C = a 2 2 ⇒ d ( C , ( S A B ) ) = a 3 2 ⇒ d ( I , ( S A B ) ) = a 3 4
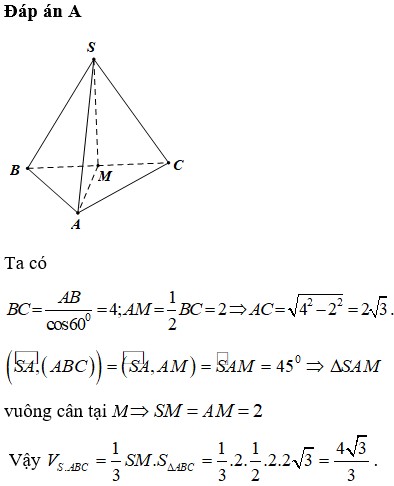
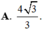
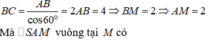
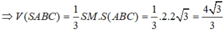

chứng minh được AH=BH -> SA= SB _> tam giác SAB cân ở S
gọi M là trung điểm của AB -> SM vuông góc với AB -> góc giữa mp (SAB) và mp (ABC) là góc SMH -> góc SMH = 60 độ
-> tìm được SH -> tìm được thể tích
tìm diên tích tam giác SAB -> khoảng cách từ C đến mp (SAB)
Vì I là trung điểm của SC nên khoảng cách từ I đến mp (SAB) bằng một nửa khoảng cách từ C đến mp (SAB)