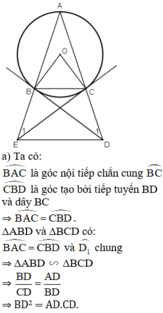
: Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp trong (O;R). Tiếp tuyến tại B và C của (O;R) cắt nhau tại D.
a) Chứng minh tứ giác OBDC nội tiếp được đường tròn.
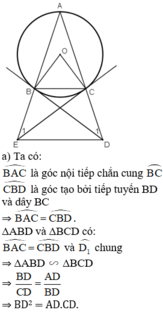
b) Đường thẳng BD và AC cắt nhau tại E. Chứng minh : EB2 = EC.EA
c) Từ điểm M trên cung nhỏ BC vẽ MI vuông góc với BC; MH vuông góc với AB ;MF vuông góc với AC.Chứng minh: H, I, F thẳng hàng.
d) Cho góc BAC = 300. Tính theo R diện tích tứ giác ABDC.

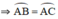
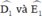 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: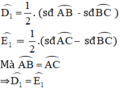

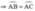
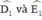 là các góc có đỉnh ở bên ngoài đường tròn nên ta có:
là các góc có đỉnh ở bên ngoài đường tròn nên ta có: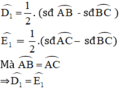

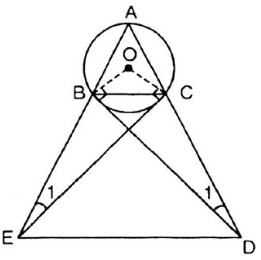


a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)