Tam giác ABC có = 1200. Tính cạnh BC cho biết cạnh AC = m và AB = n.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LN
1
Những câu hỏi liên quan
PT
1
CM
3 tháng 4 2017
Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).
SG
1
15 tháng 3 2022
Xét ΔANM và ΔABC có
AN/AB=AM/AC
\(\widehat{NAM}\) chung
Do đó: ΔANM\(\sim\)ΔABC
30 tháng 9 2021
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: \(MN=\dfrac{BC}{2}=6\left(cm\right)\)
Xét ΔABC có
M là trung điểm của AB
P là trung điểm của BC
Do đó: MP là đường trung bình của ΔBAC
Suy ra: \(MP=\dfrac{AC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Xét ΔABC có
N là trung điểm của AC
P là trung điểm của BC
Do đó: NP là đường trung bình của ΔBAC
Suy ra: \(NP=\dfrac{AB}{2}=4\left(cm\right)\)
Chu vi tam giác MNP là:
C=MN+MP+NP=4+5+6=15(cm)
18 tháng 1 2022
a: AB+BC>AC>AB-BC
=>15>AC>5
=>AC=10(cm)
=>ΔABC cân tại A
b: Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
Ta có: BC2 = AC2 + AB2 – 2AB.AC. cos1200
=> BC2 = m2 + n2 – 2m.n (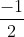
)
=> BC2 = m2 + n2 + m.n
=> BC =