Cho tam giác ABC có = 1200 cạnh b = 8cm và c = 5cm. Tính cạnh a, và góc
,
của tam giác đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
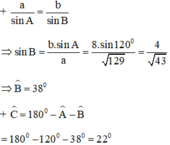

Ta có \(\widehat{A}=90^0\Rightarrow\Delta ABC\) vuông tại \(A\)
\(a,\widehat{C}=90^0-\widehat{B}=30^0\\ AC=\tan B\cdot AB=\tan60^0\cdot8=8\sqrt{3}\left(cm\right)\\ BC=\dfrac{AB}{\sin C}=\dfrac{8}{\sin30^0}=16\left(cm\right)\\ b,S_{ABC}=\dfrac{1}{2}AB\cdot AC=\dfrac{1}{2}\cdot8\cdot8\sqrt{3}=32\sqrt{3}\left(cm^2\right)\)

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{4}{5}\)
=>\(\widehat{B}\simeq53^0\)
=>\(\widehat{C}\simeq37^0\)
b: Xét ΔABC có AD là phân giác
nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
=>\(\dfrac{DB}{3}=\dfrac{DC}{4}=\dfrac{DB+DC}{3+4}=\dfrac{10}{7}\)
=>\(DB=\dfrac{30}{7}\left(cm\right);DC=\dfrac{40}{7}\left(cm\right)\)

Theo giả thiết ta có: \(A'B'=AB+3=5+3=8\left(cm\right)\).
Do \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\)
\(\Rightarrow\dfrac{AB}{A'B'}=\dfrac{AC}{A'C'}=\dfrac{BC}{B'C'}\)
\(\Rightarrow\dfrac{7}{A'C'}=\dfrac{9}{B'C'}=\dfrac{5}{8}\Rightarrow\left\{{}\begin{matrix}A'C'=\dfrac{7.8}{5}=\dfrac{56}{5}\left(cm\right)\\B'C'=\dfrac{9.8}{5}=\dfrac{72}{5}\left(cm\right)\end{matrix}\right.\).

a: XétΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< Â\)
b: \(\widehat{C}=180^0-100^0-30^0=50^0\)
Xét ΔABC có \(\widehat{B}< \widehat{C}< \widehat{A}\)
nên AC<AB<BC

\(gt\Rightarrow\widehat{B}=\widehat{I}\),\(AC=HK\)mà \(AC=5cm\Rightarrow HK=5cm\)
Trong \(\Delta ABC\)có\(\widehat{A}=70^o,\widehat{C}=50^o\)
Từ đó \(\widehat{B}=60^o\)
Mà \(\widehat{B}=\widehat{I}\Rightarrow\widehat{I}=60^o\)
Vậy \(HK=5cm,\widehat{I}=60^o\)
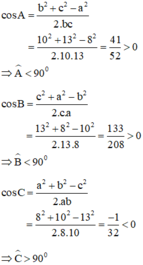
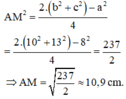
Ta có: BC2 = AC2 + AB2 – 2AB.AC. cos1200
=> BC2 = m2 + n2 – 2m.n (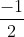 )
)
=> BC2 = m2 + n2 + m.n
=> BC =
Ta có
a2 = 82 + 52 – 2.8.5 cos 1200 = 64 + 25 + 40 = 129
=> a = √129 ≈ 11, 36cm
Ta có thể tính góc B theo định lí cosin
cosB =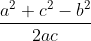 =
=  ≈ 0,7936 =>
≈ 0,7936 => 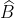 = 37048’
= 37048’
Ta cũng có thể tính góc B theo định lí sin :
cosB =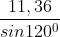 =
= 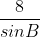 => sinB ≈ 0,6085 =>
=> sinB ≈ 0,6085 => 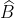 = 37048’
= 37048’
Tính C từ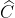 = 1800– (
= 1800– (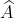 +
+ 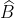 ) =>
) => 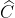 ≈ 22012’
≈ 22012’