Lập phương trình đường tròn đi qua ba điểm: M(-2; 4); N(5; 5); P(6; -2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2}\\{\left( {5 - a} \right)^2} + {\left( {2 - b} \right)^2} = {\left( {1 - a} \right)^2} + {\left( { - 3 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 3\\b = \frac{{ - 1}}{2}\end{array} \right.\)
Vậy \(I\left( {3; - \frac{1}{2}} \right)\) và \(R = IA = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2}} = \frac{{\sqrt {41} }}{2}\)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 3} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} = \frac{{41}}{4}\)
CM
12 tháng 1 2017
Gọi phương trình đường tròn (C) là: x2 + y2 – 2ax – 2by + c = 0.
a) Do A(1; 2) ∈ (C) ⇔ 12 + 22 – 2.a.1 – 2.b.2 + c = 0
⇔ 5 – 2a – 4b + c = 0 ⇔ 2a + 4b – c = 5 (1)
Do B(5; 2) ∈ (C) ⇔ 52 + 22 – 2.a.5 – 2.b.2+ c = 0
⇔ 29 – 10a – 4b + c = 0 ⇔ 10a + 4b – c = 29 (2)
Do C(1; –3) ∈ (C) ⇔ 12 + (–3)2 – 2.a.1 – 2.b.(–3) + c = 0
⇔ 10 – 2a + 6b + c = 0 ⇔ 2a – 6b – c = 10 (3)
Từ (1), (2) và (3) ta có hệ phương trình :
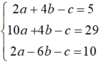
Giải hệ phương trình trên ta được nghiệm a = 3, b = –1/2, c = –1.
Vậy đường tròn đi qua ba điểm A, B, C là : x2 + y2 – 6x + y – 1 = 0.
b)
M(–2 ; 4) ∈ (C) ⇔ (–2)2 + 42 – 2.a.(–2) – 2.b.4 + c = 0 ⇔ 4a – 8b + c = –20 (1)
N(5; 5) ∈ (C) ⇔ 52 + 52 – 2.a.5 – 2.b.5 + c = 0 ⇔ 10a + 10b – c = 50 (2)
P(6; –2) ∈ (C) ⇔ 62 + (–2)2 – 2.a.6 – 2.b.(–2) + c = 0 ⇔ 12a – 4b – c = 40 (3)
Từ (1), (2) và (3) ta có hệ phương trình:
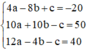
Giải hệ phương trình trên ta được nghiệm a = 2, b = 1, c = –20.
Vậy đường tròn đi qua ba điểm M, N, P là : x2 + y2 – 4x – 2y – 20 = 0.
NT
1
12 tháng 4 2016
Sử dụng phương trình đường tròn : x2 – y2 – ax – 2by +c = 0
Đường tròn đi qua điểm A(1; 2):
12 + 22 – 2a -4b + c = 0 <=> 2a + 4b – c = 5
Đường tròn đi qua điểm B(5; 2):
52 + 22 – 10a -4b + c = 0 <=> 10a + 4b – c = 29
Đường tròn đi qua điểm C(1; -3):
12 + (-3)2 – 2a + 6b + c = 0 <=> 2a – 6b – c = 10
Để tìm a, b, c ta giải hệ:
Lấy (2) trừ cho (1) ta được phương trình: 8a = 24 => a = 3
Lấy (3) trừ cho (1) ta được phương trình: -10b = 5 => b = – 0,5
Thế a = 3 ; b = -0.5 vào (1) ta tính được c = -1
Ta được phương trình đường tròn đi qua ba điểm A, B, C là :
x2 + y2 – 6x + y – 1 = 0
Chú ý:
Tâm I(x; y) của đường tròn đi qua ba điểm A, B, C là điểm cách đều ba điểm ấy, hay
IA = IB = IC => IA2 = IB2 = IC2
Từ đây suy ra x, y là nghiệm của hệ:
<=> I(3; )
Từ đây ta tìm được R và viết được phương trình đường tròn.
TL
0
MN
3 tháng 6 2021
c)
(d) vuông góc với (d') : y = 2x
=> (d) có dạng : y = -2x + b
(d) đi qua M (3,5) :
5 = (-2) . 3 + b
=> b = 10
(d) : y = -2x + 10
12 tháng 4 2016
Đường tròn tiếp xúc với hai trục tọa độ nên tâm I của nó phải cách đều hai trục tọa độ. Đường tròn này lại đi qua điểm M(2 ; 1), mà điểm M này lại là góc phần tư thứ nhất nên tọa độ của tâm I phải là số dương.
xI= yI > 0
gọi xI= yI = a. Như vậy phương trình đường tròn cần tìm là :
(2 – a)2 + (1 – a)2 = a2
a2 – 6a + 5 = 0 => a = 1 hoặc a = 5
Từ đây ta được hai đường tròn thỏa mãn điều kiện
+ Với a = 1 => (C1) => (x – 1 )2 + (y – 1)2 = 1
x2 + y2 – 2x – 2y + 1 = 0
+ Với a = 1 => (C2) => (x – 5 )2 + (y – 5)2 = 25
x2 + y2 – 10x – 10y + 25 = 0
Ta tính được I(2; 1), R= 5
Phương trình đường tròn đi qua ba điểm M(-2; 4); N(5; 5); P(6; -2) là:
(x – 2)2 + (y – 1)2 = 25 <=> x2 – y2 – 4x – 2y – 20 = 0