tìm số dư của phép chia 5^2015 chia cho 53
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
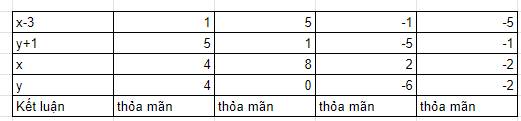
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.

Olm chào em, đây là toán nâng cao chuyên đề phép chia có dư, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Số dư là số dư lớn nhất có thể nên số dư là:
5 - 1 = 4
Số bị chia của phép chia đó là:
2015 x 5 + 4 = 10079
Đáp số: 10079
ƯCLN(5,53)=1 nên theo định lí Fermat, ta được:
552\(\equiv\)1 (mod 53)
=> (552)38 \(\equiv\) 51976 \(\equiv\)1 (mod 53) (1)
Ta có: 513 \(\equiv\) 23 (mod 53)
=> (513)3 \(\equiv \) 539 \(\equiv\) 233 \(\equiv\)30 (mod 53) (2)
Nhân (1) và (2) với nhau, ta được:
51976 .539 \(\equiv\) 1.30 \(\equiv \)30 (mod 53)
=>52015 \(\equiv\)30 (mod 53)
Vậy 52015 chia 53 dư 30
Đây là ý kiến của mình, có gì sai sót mong bạn bỏ qua
bạn dùng đồng dư là được