Năng lượng ion hóa nguyên tử hiđrô lav13,6eV . Bước sóng ngắn nhất của bức xạ mà nguyên tử hiđrô có thể phat ra la
A 0,1220μm
B 0,0913μm
C. 0,0656μm
D. 0,5672μm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
violet
Giáo viên
19 tháng 4 2016
Năng lượng ion hóa là năng lượng tối thiểu để có thể tách một electron ra khỏi nguyên tử để trở thành electron tự do.
Khi nguyên tử hiđrô hấp thụ năng lượng bằng 13,6 eV thì năng lượng của nguyên tử lúc này là 0 eV ứng với việc nó có thể phát ra một phôtôn có bước sóng ngắn nhất thỏa mãn
\(\frac{hc}{\lambda}= E_0-E_1 = 0-(-13,6)= 13,6 eV.\)
=> \(\lambda _ {min}= \frac{6,625.10^{-34}.3.10^8}{13,6.1,6.10^{-19}}= 9,13.10^{-8}m= 0,0913 \mu m..\)
Q
19 tháng 4 2016
Năng lượng ion hóa là năng lượng tối thiểu để có thể tách một electron ra khỏi nguyên tử để trở thành electron tự do.
Khi nguyên tử hiđrô hấp thụ năng lượng bằng 13,6 eV thì năng lượng của nguyên tử lúc này là 0 eV ứng với việc nó có thể phát ra một phôtôn có bước sóng ngắn nhất thỏa mãn
hc/λ=E0−E1=0−(−13,6)=13,6eV.
=> λmin=6,625.10−34.3.10813,6.1,6.10−19=9,13.10−8m=0,0913μm..
VT
28 tháng 6 2018
+ Khi nguyên tử ở trạng thái kích thích chuyển về trạng thái cơ bản có thể phát ra tối đa 15 bức xạ nên
+ Bước sóng lớn nhất ứng với sự chuyển của electron từ P n = 6 về O n = 5
+ Bước sóng bé nhất ứng với sự chuyển của electron từ P n = 6 về K n = 1
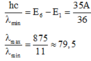
=> Chọn A.
bước sóng ngắn nhất của hidro là bước sóng từ lớp \(\infty\) về lớp K
sử dụng công thức
R\(\infty\) x (\(\frac{1}{1^2}\) - \(\frac{1}{\infty}\)) = \(\frac{1}{10973731,57}\)
=> \(\lambda=\frac{1}{10973731,57}\) = \(^{9,11.10^{-8}}\)m \(\approx\) 0,0913 \(\mu m\)
=> đáp án B
ở đây tớ chỉ giải mẹo theo công thức đó. muốn biết thêm cách giải mẹo này thì cmt nhé!!