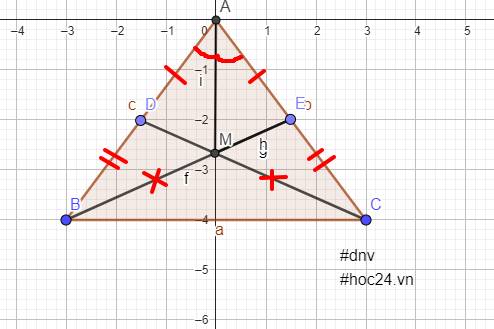
Cho tam giác ABC cân tạ A,kẻ đường cao BE, trên AB lấy D sao cho AE=AD. Gọi H là giao điểm của BE và CD
a) CM: tam giác ABE= tam giác ACD
b) CM: H là trực tâm của ttam giác ABC
c) gọi M là trung điểm của BC, CM 3 điểm A,M,H thẳng hàng
d) Cm: BC=2DM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LA
11 tháng 5 2017
Xét tg ABE va tg ACD, co
+/Goc A chung
+/AB=AC [vi tg ABC can]
+/AD=AE[GT]
Vay tgABE=tgACD [c.g.c]
Suy ra góc AEB=góc ADC[vì là hai cạnh tương ứng]
Mà góc AEB=90[độ theo gt]
suy ra góc ADC=90[độ vì cũng bằng với góc AEB]
Hãy cạnh ĐC là đường cao
2 đường cao ĐC và BÈ cùng đi qua điểm H
Vậy H chính là đường trung trực của tg cân ABC
[NẾU BÀI CỦA MÌNH ĐÚNG HAY TÍCH ĐỂ NHÉ]
30 tháng 4 2023
a: Xét ΔAEBvà ΔADC có
AE=AD
góc A chung
AB=AC
=>ΔAEB=ΔADC
=>BE=CD
b: Xét ΔMDB và ΔMEC có
góc MDB=góc MEC
DB=EC
góc MBD=góc MCE
=>ΔMDB=ΔMEC
c: Xét ΔAMB và ΔAMC có
MA chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
1 tháng 5 2023
`@`` \text {dnv}`
`a,`
Xét `\Delta ABE` và `\Delta ACD`:
`\text {AB = AC (Tam giác ABC cân tại A)}`
`\hat {A}`` \text {chung}`
`\text {AD = AE (gt)}`
`=> \Delta ABE = \Delta ACD (c-g-c)`
`-> \text {BE = CD (2 cạnh tương ứng)}`
`b,`
Vì `\Delta ABE = \Delta ACD (a)`
$ -> \widehat {ACD} = \widehat {ABE} (\text {2 góc tương ứng})$
`->` $\widehat {ADC} = \widehat {AEB} (\text {2 góc tương ứng})$
Ta có: \(\left\{{}\begin{matrix}\widehat{ADC}+\widehat{BDC}=180^0\\\widehat{AEB}+\widehat{CEB}=180^0\end{matrix}\right.\)
$\widehat {ADC} = \widehat {AEB}$
`->` $\widehat {CEB} = \widehat {BDC}$
Ta có:\(\left\{{}\begin{matrix}\text{AB = AD + DB}\\\text{AC = AE + EC}\end{matrix}\right.\)
Mà: \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{AD = AE}\end{matrix}\right.\)
`-> \text {BD = EC}`
Xét `\Delta BMD` và `\Delta CME`:
\(\widehat{\text{DBM}}=\widehat{\text{ECM}}\left(\text{CMT}\right)\)
\(\text{BD = CE (CMT)}\)
\(\widehat{\text{BDM}}=\widehat{\text{CEM}\text{ }}\text{ }\left(\text{CMT}\right)\)
`=> \Delta BMD = \Delta CME (g-c-g)`
`c,` Đề có phải là "Chứng minh AM là phân giác của góc BAC" ?
Vì `\Delta BMD = \Delta CME (b)`
`-> \text {MB = MC (2 cạnh tương ứng)}`
Xét `\Delta BAM` và `\Delta CAM`:
`\text {AB = AC} (\Delta ABC \text {cân tại A})`
`\text {AM chung}`
`\text {MB = MC (CMT)}`
`=> \Delta BAM = \Delta CAM (c-c-c)`
`->` $\widehat {BAM} = \widehat {CAM} (\text {2 góc tương ứng})$
`-> `\(\text{AM là tia phân giác của }\widehat{\text{BAC}}\)
27 tháng 4 2023
a: Xét ΔBAE và ΔBME có
BA=BM
AE=ME
BE chung
=>ΔBAE=ΔBME
b: Xet ΔBAK và ΔBMK có
BA=BM
góc ABK=góc MBK
BK chung
=>ΔBAK=ΔBMK
=>góc BMK=90 độ
=>MK vuông góc AC
c: Xét tứ giác KFMQ có
MF//KQ
MF=KQ
=>KFMQ là hình bình hành
=>MQ//FK
=>góc CMQ=góc CBK=góc ABK
12 tháng 8 2023
a: O là giao điểm của 3 đường trung trực của ΔABC
=>O là tâm đường tròn ngoại tiếp ΔABC
=>AM là đường kính của (O)
Xét (O) có
ΔABM nội tiếp đường tròn
AM là đường kính
=>ΔABM vuông tại B
=>BM vuông góc AB
=>BM//CH
Xét (O) có
ΔACM nội tiếp
AM là đường kính
=>ΔAMC vuông tại C
=>AC vuông góc CM
=>CM//BH
Xét tứ giác BHCM có
BH//CM
BM//CH
=>BHCM là hình bình hành
=>BC cắt HM tại trung điểm của mỗi đường
=>I là trung điểm của HM
b: Xét ΔMAH có
O,I lần lượt là trung điểm của MA,MH
=>OI là đường trung bình
=>OI//AH và OI=1/2AH
=>AH=2OI
27 tháng 2 2021
a) Xét ΔABE vuông tại A và ΔACD vuông tại A có
AB=AC(ΔABC vuông cân tại A)
AE=AD(gt)
Do đó: ΔABE=ΔACD(cạnh huyền-cạnh góc vuông)
Suy ra: BE=CD(Hai cạnh tương ứng)
28 tháng 4 2023
a: Xet ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
góc BAD=góc EAD
=>ΔABD=ΔAED
=>AB=AE và DB=DE
=>AD là trung trực của BE
b: Xét ΔAEF vuông tại E và ΔABC vuông tại B có
AE=AB
góc EAF chung
=>ΔAEF=ΔABC
=>AF=AC
Xet ΔADF và ΔADC có
AD chung
góc DAF=góc DAC
AF=AC
=>ΔADF=ΔADC
c: ΔCBF vuông tại B
mà BM là trung tuyến
nên MB=MF
câu a
tam giác abc cân a
=> ab = ac (tính chất)
tam giác abe và tam giác acd có
chung góc a
ab=ac
ad=ae
=> tam giác abe = tam giác acd (cgc)
câu b
từ câu a
=> góc e = góc d
mà góc e = 90 độ
=> góc d = 90 độ
=> cd là đưòng cao
tam giác abc có đưòng cao be và cd giao tại h
=> h là trực tâm
câu c
từ câu b
=> ah là đường cao
=> ah đồng thời là đường trung tuyến
mà am là đường trung tuyến
=> ah trùng am
=> a,m,h thẳng hàng
câu d
tam giác cbd vuông tại d có dm là đưòng trung tuyến ứng với cạnh huyền bc
\(dm=\dfrac{bc}{2}\\ =>bc=2.dm\)
chúc may mắn :)