\(_{11}^{24}Na\) là chất phóng xạ với chu kỳ bán rã 15 giờ. Ban đầu có một lượng \(_{11}^{24}Na\) thì sau một khoảng thời gian bao nhiêu lượng chất phóng xạ trên bị phân rã 75 % ?
A.7h30'.
B.15h00'.
C.22h30'.
D.30h00'.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
9 tháng 4 2017
Đáp án A
Phương pháp:
Áp dụng công thức tính khối lượng bị phâṇ rã sau phản ứng
Theo bài ra tra có:
CM
31 tháng 1 2019
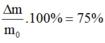
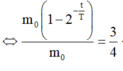
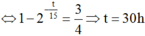
Đáp án A.
Ta có:
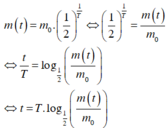
Theo giả thiết ta có:
T = 1602(năm), m 0 = 1 g r a m , m t = 0.5 g r a m
Áp dụng công thức ta có khoảng thời gian cần tìm là:
t = T . log 1 2 m t m 0 = 1602. log 1 2 0.5 1 = 1602. log 1 2 1 2 = 1602
Vậy sau 1602 năm thì 1gram chất phóng xạ này bị phân ra còn lại 0.5 gram
H
23 tháng 3 2016
Tỉ số giữa độ phóng xạ sau 11,4 ngày và độ phóng xạ ban đầu
\(\frac{H}{H_0}= 2^{-\frac{t}{T}}=2^{-\frac{11,4}{3,8}}= 0,125. \)
=> Độ phóng xạ sau 11,4 ngày chiếm 12,5 % độ phóng xạ ban đầu
VT
8 tháng 8 2017
Đáp án C
Lượng chất còn lại là:
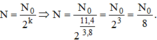
Vậy lượng chất phóng xạ còn lại chiếm 12,5% so với độ phóng xạ của lượng chất phóng xạ ban đầu.
VT
15 tháng 12 2017
Đáp án: A
Lượng Co đã bị phân rã:
m’ = m0 - m = m0.(1- 1/21/5,33) = 0,122m0 = 12,2%.m0
VT
15 tháng 3 2018
∆ t là khoảng thời gian để số hạt nhân của một lượng chất phóng xạ giảm đi e lần:
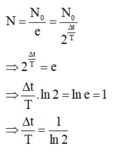
Sau khoảng thời gian 0 , 51 ∆ t chất phóng xạ còn lại
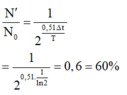
Đáp án B
Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)
D. 30h00'