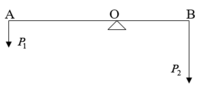
Thanh AB đồng chất, tiết diện đều, dài 150cm, ở đầu A người ta treo một vật có khối lượng m1=3 kg. Ở đầu B người ta treo vật thứ hai có khối lượng m2= 6kg thì thấy hệ thống cân bằng. Hãy xác định điểm tựa O của thanh AB nói trên ( bỏ qua khối lượng của thanh )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


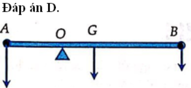
Dễ thấy, nếu O nằm giữa G và B thì thanh không thể cân bằng nên O nằm giữa A và G. Quy tắc mômen lực đối với trục qua O:
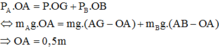

Dễ thấy, nếu O nằm giữa G và B thì thanh không thể cân bằng nên O nằm giữa A và G. Quy tắc mômen lực đối với trục qua O:

Ta có:
P = m g = 2.10 = 20 ( N ) ; P A = m A . g = 5.10 = 50 ( N ) ; P B = m B . g = 1.10 = 10 ( N )
Theo điều kiện cân bằng Momen lực: MA = MP + MB
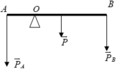
⇒ P A . O A = P . O G + P B . O B
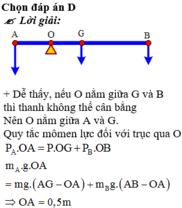
AG = GB = 1m
OG = AG – OA = 1 – OA
OB = AB – AO = 2 – OA
=> 50. OA = 20 (1- OA) + 10( 2 – OA )
=> OA = 0,5m

Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
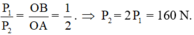
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)

Đáp án B
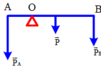
Áp dụng quy tắc momen lực: MA = MP + MB
↔ P1. OA = P. OI + P2. OB
AI = IB = 1m
OI = AI – OA = 1 – OA
OB = OI – IB = 2 – OA
↔ 50. OA = 20 (1- OA) + 10(2 – OA) → OA = 0,5m.

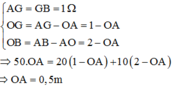
gọi l1 là chiều dài cánh tay đòn 1 ( ở đây là OA) l2 là chiều dài cánh tay đòn 2 ( ở đây là OB)
l1+l2=150 cm =1,5 m (1)
m1=3kg => P1=30(N)
m2=6kg => P2=60(N)
Để hệ thống cân bằng thì:
m1.l1=m2.l2
=> 30l1=60l2 => l1 - 2l2= 0 ( đơn giản mỗi vế cho 30) (2)
Từ (1) và (2) ta có hệ phương trình
l1+l2=1,5
l1 - 2l2=0
=> l1=1 (m)
l2=0,5(m)
vậy điểm O cách A 100 cm cách B 50cm