Một xilanh đặt nằm ngang, hai đầu kín, có thể tích 2V0 và chứa khí lí tưởng ở áp suất p0. Khí trong xilanh được chia thành hai phần bằng nhau nhờ một pit-tông mỏng, cách nhiệt có khối lượng m. Chiều dài của xilanh là 2l. Ban đầu khí trong xilanh có nhiệt độ là T0, pit-tông có thể chuyển động không ma sát dọc theo xi lanh.
a Nung nóng chậm một phần khí trong xilanh để nhiệt độ tăng thêm \(\Delta\)T và làm lạnh chậm phần còn lại để nhiệt độ giảm đi \(\Delta\)T. Hỏi pit-tông dịch chuyển một đoạn bằng bao nhiêu khi có cân bằng?
b. Đưa hệ về trạng thái ban đầu (có áp suất p0, nhiệt độ T0). Cho xilanh chuyển động nhanh dần đều theo phương ngang dọc theo trục của xi lanh với gia tốc a thì thấy pit-tông dịch chuyển một đoạn x so với vị trí cân bằng ban đầu. Tìm gia tốc a. Coi nhiệt độ không đổi khi pit-tông di chuyển và khí phân bố đều

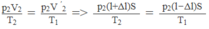
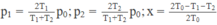
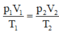
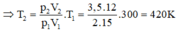
a) Phần xi lanh bi nung nóng: \(\frac{P_oV_o}{T_o}=\frac{P_1V_1}{T_1}=\frac{P_1V_1}{T_0+\Delta T}\)
Phần xi lanh bị làm lạnh: \(\frac{P_oV_o}{T_o}=\frac{P_2V_2}{T_2}=\frac{P_2V_2}{T_0-\Delta T}\)
Vì P1 = P2 \(\rightarrow\frac{V_1}{V_2}=\frac{T_0+\Delta T}{T_0-\Delta T}\) (1)
Gọi đoạn di chuyển của pit-tông là x, ta có: V1 = (l + x)S và V2 = (l - x)S (2)
Từ (1) và (2) ta có \(\frac{\left(l+x\right)S}{\left(l-x\right)S}=\frac{T_0+\Delta T}{T_0-\Delta T}\rightarrow\) x = \(\frac{l\Delta T}{T_0}\)
b) P2V2 = P0V \(\rightarrow\) P2 = P0V0 /(l - x)S (1)
P1V1 = P0V \(\rightarrow\) P2 = P0V0/(l + x)S (2)
Xét pit-tông: F2 - F1 = ma \(\rightarrow\) (P2 - P1)S = ma (3)
Từ (1), (2), và (3)
\(\left(\frac{P_0V}{S\left(l-r\right)}\right)-\left(\frac{P_0V}{S\left(l+r\right)}\right)S\)= ma \(\rightarrow\) a = 2P0V0x/(l2 – x2)m