Giải giúp em phầm III ạ em cám ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



cái này áp dụng hệ thức lượng thôi bạn
AH=căn 6^2-4,8^2=3,6cm
=>AC=6^2/3,6=10cm


Từ đồ thị \(f'\left(x\right)\) ta có BBT hàm \(f\left(x\right)\) như sau:
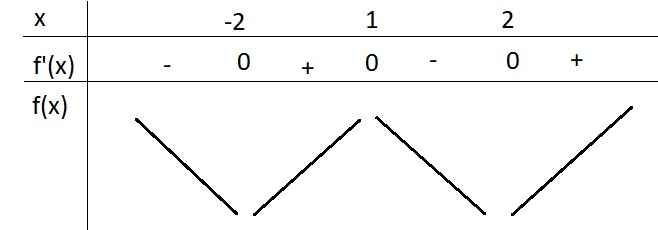
Từ đó ta thấy hàm \(f\left(x\right)\) đồng biến trên các khoảng \(\left(-2;1\right)\) và \(\left(2;+\infty\right)\)
Cũng từ BBT, trên \(\left[-2;2\right]\) ta thấy \(\max\limits_{\left[-2;2\right]}f\left(x\right)=f\left(1\right)\)
Diện tích giới hạn bởi phần đồ thị \(f'\left(x\right)\) và trục hoành trên \(\left[-2;1\right]\) lớn hơn đoạn \(\left[1;2\right]\)
\(\Rightarrow\int\limits^1_{-2}\left|f'\left(x\right)\right|dx>\int\limits^2_1\left|f'\left(x\right)\right|dx\Rightarrow\int\limits^1_{-2}f'\left(x\right)dx>\int\limits^1_2f'\left(x\right)dx\)
\(\Rightarrow f\left(1\right)-f\left(-2\right)>f\left(1\right)-f\left(2\right)\)
\(\Rightarrow f\left(2\right)>f\left(-2\right)\)
\(\Rightarrow\min\limits_{\left[-2;2\right]}f\left(x\right)=f\left(-2\right)\)
\(\Rightarrow a+b=1+\left(-2\right)=-1\)

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.



 Giúp em giải mà không áp dụng ĐỊNH LÝ HÀM SIN với ạ. Tại em chưa học!!!
Giúp em giải mà không áp dụng ĐỊNH LÝ HÀM SIN với ạ. Tại em chưa học!!! 
 ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn
ai giúp em với ạ :<< em đang cần gấp lắm, giải hộ em 2 bài thì càng tốt ạ, em xin chân thành cám ơn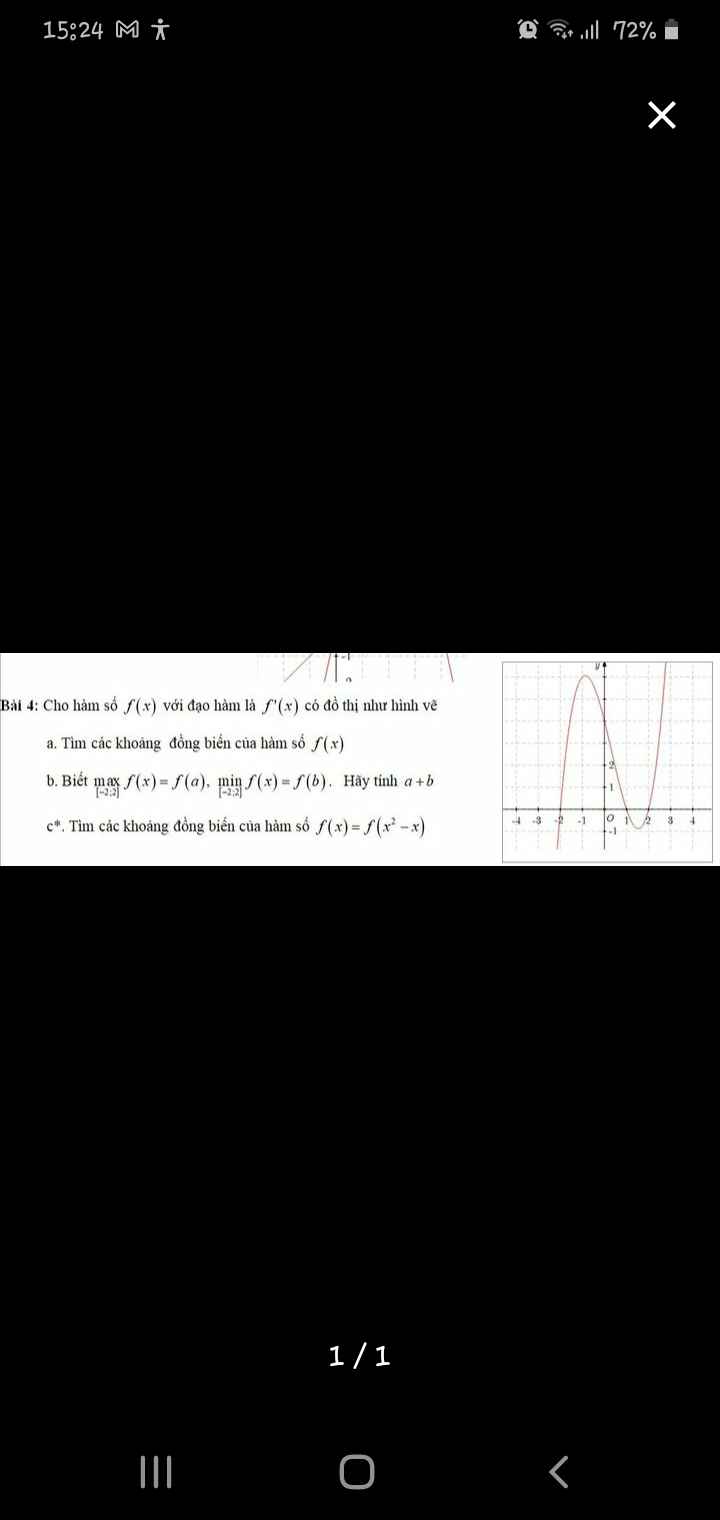


Phần 3
Câu 1 B
Câu 2 B
Câu 3 D
Câu 4 B
Câu 5 B
THAM KHẢO!
III. Phần tập làm văn
1B
2C
3C
4A
5B