M=x6-y5+x4y4+1 có bậc bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2017
Đa thức M có 3 hạng tử và bậc của chúng lần lượt là:
x6 có bậc 6
– y5 có bậc 5
x4y4 có bậc 4+4 = 8
Bậc 8 là bậc cao nhất
⇒ Đa thức M là đa thức bậc 8
Như vậy :
- Bạn Thọ và Hương nói sai.
- Nhận xét của bạn Sơn là đúng
- Câu trả lời đúng : Đa thức M có bậc là 8.
CM
4 tháng 11 2018
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
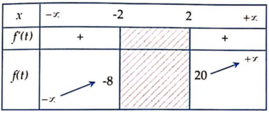
Bảng biến thiên:
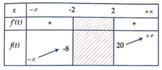
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
23 tháng 10 2023
2D
6
\(x^3+125=\left(x+5\right)\left(x^2-5x+25\right)\)
A là đa thức bậc 1
=>A=x+5
=>B=x^2-5x+25
=>Chọn A
KV
23 tháng 10 2023
Câu 2. M có bậc 2 + 7 = 9
Chọn D
Câu 6. x³ + 125 = x³ + 5³ = (x + 5)(x² - 5x + 25)
Chọn A
25 tháng 3 2021
a) \(5x^2y^3z\cdot\left(-11xyz^4\right)=\left(-11\cdot5\right)\cdot\left(x^2\cdot x\right)\cdot\left(y^3\cdot y\right)\cdot\left(z\cdot z^4\right)=-55x^3y^4z^5\)
Phần biến: \(x^3y^4z^5\)
Hệ số: -55
Bậc của đơn thức: 12
b) \(-6x^4y^4\cdot\left(\dfrac{-2}{3}x^5y^3z^2\right)=\left(-6\cdot\dfrac{-2}{3}\right)\cdot\left(x^4\cdot x^5\right)\cdot\left(y^4\cdot y^3\right)\cdot z^2=4x^9y^7z^2\)
Phần biến: \(x^9y^7z^2\)
Hệ số: 4
Bậc của đơn thức: 18
T2
25 tháng 3 2021
a) 5x2y3z⋅(−11xyz4)=(−11⋅5)⋅(x2⋅x)⋅(y3⋅y)⋅(z⋅z4)=−55x3y4z55x2y3z⋅(−11xyz4)=(−11⋅5)⋅(x2⋅x)⋅(y3⋅y)⋅(z⋅z4)=−55x3y4z5
Phần biến: x3y4z5x3y4z5
Hệ số: -55
Bậc của đơn thức: 12
b) −6x4y4⋅(−23x5y3z2)=(−6⋅−23)⋅(x4⋅x5)⋅(y4⋅y3)⋅z2=4x9y7z2−6x4y4⋅(−23x5y3z2)=(−6⋅−23)⋅(x4⋅x5)⋅(y4⋅y3)⋅z2=4x9y7z2
Phần biến: x9y7z2x9y7z2
Hệ số: 4
Bậc của đơn thức: 18
NM
Nguyễn Minh Quang
Giáo viên
11 tháng 9 2021
ta có :
\(-7x^6-x^4y^4+3x^5+5x^6+x^4y^4-1=-2x^6+3x^5-1\)
nên bậc của đa thức là bậc 6
11 tháng 9 2021
Bậc của đa thức – 7x6 – x4y4 + 3x5 +5x6 – 2x+2x6 + x4y4– 1 là:
A. 5 B. 6 C. 8 D. 4
CM
5 tháng 8 2019
Chọn đáp án D.
Bất phương trình tương đương với
trong đó hàm số f t = t 3 + 3 t đồng biến trên R
Vậy y c b t ⇔ x 2 - m x + 1 ≥ 0 , ∀ x
Có 5 số nguyên thoả mãn
CM
7 tháng 2 2017
Bất phương trình tương đương với:
trong đó hàm số f ( t ) = t 3 + 3 t đồng biến trên R.
Vậy 
Có 5 số nguyên thoả mãn.
Chọn đáp án D.
Đa thức M có bậc là 8