Một con lắc gồm một quả cầu được treo vào một sợi dây không dãn chiều dài là \(l\). Kéo quả cầu từ vị trí cân bằng tới vị trí lệch với phương thẳng đứng góc 300 rồi thả ra.
a) Tính vận tốc quả cầu khi đi qua vị trí cân bằng ( hình vẽ)
b) Chứng minh rằng vận tốc này có độ lớn cực đại. 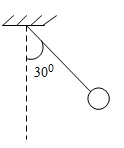
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/2.m v 2 m a x = mgl(1 - cos α 0 )
![]()
F - mg = m v 2 m a x /l ⇒ F = m(g + v 2 m a x /l)
F = 0,05(9,8 + 2 , 3 2 /2) ≈ 0,62N

Đáp án C
+ Tần số góc của dao động
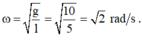 .
.
+ Gốc thời gian được chọn là lúc con lắc đi qua vị trí cân bằng lần thứ 2 =>qua vị trí cân bằng theo chiều dương 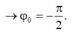
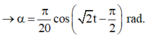

a) Chọn gốc thế năng trọng trường tại C ( Hình 92).
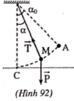
Theo định luật bảo toàn cơ năng: W A = W M
![]()
Vận tốc của m tại một điểm trên quỹ đạo ( ứng với góc lệch α )
![]()
Vận tốc v sẽ đạt cực đại khi cos α = 1 hay α = 0 .
![]()
b) Phương trình chuyển động của m: P → + T → = m a →
Chiếu phương trình lên phương bán kính đi qua M, chiều dương hướng vào điểm treo:
![]()
Thay ![]() vào phương trình của T ta được:
vào phương trình của T ta được:
Lực căng dây tại M ( ứng với góc lệch: T = m g 3 cos α - 2 cos α 0
Lực căng T đạt cực đại khi cos α = 1 hay α = 0 : T = m g 3 - 2 cos α 0

Đáp án B
Lực căng của sợi dây tại vị trí cân bằng
T = m g 3 - 2 cos α 0 ≈ 0 , 62 N

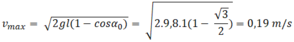

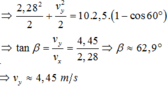


a) \(v=\sqrt{2gl\left(1-\cos\alpha\right)}\)
b) Tại vị trí này, toàn bộ thế năng ban đầu của con lắc đã chuyển hóa thành động năng, còn ở các vị trí khác chỉ một phần thế năng ban đầu chuyển hóa thành động năng. Do đó, vận tốc tại vị trí này là cực đại.