cho 2 đường thẳng tt' và zz' cắt nhau tạo ra những cặp góc đối đỉnh tOz và t'Oz', biết tOz'= 4. tOz. Tính các góc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 10 2018
Chọn đáp án D
Cách 1: Thay tọa độ điểm M vào phương trình của d
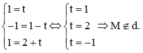
Thay tọa độ điểm N vào phương trình của d.
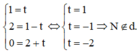
Thay tọa độ điểm P vào phương trình của d.
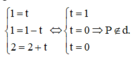
Vậy Thật vậy, thay tọa độ điểm Q vào phương trình d
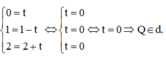
Cách 2: Quan sát thấy ba điểm M, N, P đều có hoành độ bằng 1.
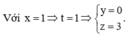
Suy ra M, N, P đều không thuộc d. Do đó đáp án đúng là D.
23 tháng 9 2015
(Bạn tự ghi số đọ và tên đường thẳng nhé. Mình ngại lắm)
Vì tt` cắt xx` tại A nên xAt và tAx` là 2 góc kề bù mà tAx`=138o nên xAt=180-138=42o
Vì xAt và tBy là 2 góc đồng vị bằng nhau mà xAt=yBt nên xx` và yy` là 2 đường thẳng song song
CC
13 tháng 1 2019
_ Chọn 1 điểm làm điểm thứ nhất ta vẽ được 19 đường thẳng đi qua điểm đó và 19 điểm còn lại.
Đây mình vẽ minh họa cho bạn dễ hiểu :
\(\Rightarrow\)Có thể chọn 20 cách cho điểm thứ nhất như vậy .
_ Như vậy ta đã vẽ 20 . 19 đường thẳng và mỗi đường thẳng đc vẽ hai lần .
Từ đó \(\Rightarrow\)Từ 20 điểm phân biệt , ta vẽ được 20 . 19 : 2 = 190 ( đth )
CM
21 tháng 10 2017
d : x = t y = 2 - t z = 4 + t t ∈ R có vectơ chỉ phương u 1 → ( 1;-1;1 )
Đáp án cần chọn là C
hình vẽ bạn ơi
Ta có: \(\widehat{tOz'}+\widehat{tOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow5\cdot\widehat{tOz}=180^0\)
\(\Leftrightarrow\widehat{tOz}=36^0\)
\(\Leftrightarrow\widehat{tOz'}=144^0\)
\(\widehat{z'Ot'}=36^0\); \(\widehat{zOt'}=144^0\)