cho csc (un) tổng ba số hạng đầu tiên =-6 và tổng các bình phương của chúng = 30. hãy tìm csc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 2 2016
Gọi 6 số hạng cấp số cộng là a,a+d,a+2d,...,a+5d. Suy ra
a+(a+d)+(a+2d)+...(a+4d)=5a+(1+2+3+4)d=5a+10d=31
a+d+(a+2d)+(a+3d)+...(a+5d)=5a+(1+2+3+4+5)d=5a+15d=62
Suy ra \(d=\dfrac{31}{5},a=-\dfrac{31}{5}\)
CM
20 tháng 1 2018
Chọn B
Gọi ba số hạng liên tiếp của cấp số cộng là a - 2x; a ; a+2x với công sai d=2x.
Theo giả thiết ta có:
a − 2 x + a + a + 2 x = − 9 ( a - 2 x ) 2 + a 2 + a + 2 x 2 = 29 ⇔ 3 a = − 9 3 a 2 + 8 x 2 = 29 ⇔ a = − 3 8 x 2 = 2 ⇔ a = − 3 x = ± 1 2
với
x = 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. 1 2 = − 4
với
x = − 1 2 ⇒ u 1 = a − 2 x = − 3 − 2. − 1 2 = − 2
Vậy số hạng đầu tiên là -4 hoặc -2
AH
Akai Haruma
Giáo viên
17 tháng 3 2021
Lời giải:
Ta có:
$u_n=9-5n; u_{n+1}=9-5(n+1)$
$\Rightarrow u_{n+1}-u_n=-5$ là hằng số
Do đó $(u_n)$ là cấp số cộng với công sai $d=-5$
$u_1=9-5.1=4$
Giả sử $-9991$ là số hạng của scs nói trên.
Khi đó:
$-9991=u_k=9-5k\Rightarrow k=2000$
$\Rightarrow -9991$ là số hạng thứ $2000$
Còn $2016$ hiển nhiên không phải số hạng của csc vì $u_n=9-5n\leq 4$ với mọi $n\in\mathbb{N}\geq 1$
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 2 2020
a/ Đề vẫn giống cũ, kết quả rất xấu nên chắc chắn sai (vì các số hạng nguyên nên \(u_1\) và d đều phải nguyên, do đó nghiệm của pt phải đẹp)
b/ \(\left\{{}\begin{matrix}u_1+d-\left(u_1+2d\right)+u_1+4d=10\\u_1+3d+u_1+5d=26\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+3d=10\\2u_1+8d=26\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\)
\(\Rightarrow u_{10}=u_1+9d=1+9.3=28\)
c/ \(\left\{{}\begin{matrix}S_7=\frac{7\left(2u_1+6d\right)}{2}=63\\\left(u_1+3d\right)\left(u_1+5d\right)=117\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1+3d=9\\u_1^2+8u_1d+15d^2=117\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}u_1=9-3d\\u_1^2+8u_1d+15d^2=117\end{matrix}\right.\)
\(\Rightarrow\left(9-3d\right)^2+8d\left(9-3d\right)+15d^2-117=0\)
\(\Leftrightarrow18d-36=0\Rightarrow d=2\Rightarrow u_1=3\)
Đó, 2 bài sau đề đúng là kết quả đẹp liền
AH
Akai Haruma
Giáo viên
9 tháng 11 2023
Lời giải:
Đặt $u_2=a$.
$u_2^2+u_3^2+u_4^2=a^2+(a-3)^2+(a-6)^2=3a^2-18a+45$
$=3(a-3)^2+18\geq 18$
Vậy $u_2^2+u_3^2+u_4^2$ đạt min =18 khi $a-3=0\Leftrightarrow a=3$
Tổng 100 số hạng đầu tiên:
$S_{100}=u_1+u_2+u_3+...+u_{100}$
$=(u_2-d)+u_2+(u_2+d)+(u_2+2d)+...+(u_2+98d)$
$=100u_2+(-1+0+1+2+...+98)d$
$=100.3+4850(-3)=-14250$
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 2 2020
a/ Bạn coi lại đề, vế phải sao lại \(102-2\), lớp 3 lớp 4 người ta cho kiểu này còn có lý, chứ lớp 11 chắc chẳng ai cho kiểu vầy cả, nó... ngớ ngẩn quá
b/ Giống câu bạn vừa đăng
CM
9 tháng 5 2017
Chọn A
Giả sử bốn số hạng đó là a − 3 x ; a − x ; a + x ; a + 3 x với công sai là d =2x. Khi đó, ta có:
a − 3 x + a − x + a + x + a + 3 x = 20 a − 3 x 2 + a − x 2 + a + x 2 + a + 3 x 2 = 120
⇔ 4 a = 20 4 a 2 + 20 x 2 = 120 ⇔ a = 5 x = ± 1
Vậy bốn số cần tìm là 2; 4; 6; 8.
Tổng của 2 số hạng đầu tiên là: 2+ 4= 6.
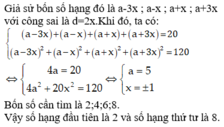
Gọi số hạng đầu tiên là a, công sai là d. 3 số hạng đầu là a,a+d.a+2d
a+(a+d)+(a+2d)=3a+3d=-6 nên d=-a-2
Suy ra 3 số hạng đầu là a, -2, -a-4
\(a^2+(-2)^2+(-a-4)^2=2a^2+8a+20=30\)
nên a=1,d=-3 hoặc a=-5,d=3