Giúp em bài 13 14 với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 2 2023
Bài 13:
góc A=180-80-30=70 độ
=>góc BAD=góc CAD=70/2=35 độ
góc ADC=80+35=115 độ
góc ADB=180-115=65 độ
7 tháng 2 2023
Bài 14:
Xét ΔABC vuông tại A
-> \(\widehat{B}\)\(+ \widehat{C}=90^o\)
Mà \(\widehat{B}=\widehat{C}\)
=> \(2\widehat{B}=90^o\)
=> \(\widehat{B}=45^o\)
giải giúp em bài 11 12 13 của bài 14 đi ạ
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
11.
\(=\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{x-9}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}-2}{3+\sqrt{x}}\)
AH
Akai Haruma
Giáo viên
26 tháng 6 2021
12.
\(=\frac{(3-\sqrt{x})(3\sqrt{x}-2)+(5\sqrt{x}+7)(3\sqrt{x}+4)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+52\sqrt{x}+22}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+10\sqrt{x}-12}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(3\sqrt{x}-2)(2\sqrt{x}+3)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(2\sqrt{x}+3)}{5\sqrt{x}+7}\)
17 tháng 8 2021
Bài 13:
nO2= 32/32=1(mol)
a) PTHH: 2 Mg + O2 -to-> 2 MgO
nMg=nMgO=nO2.2=2(mol)
=> mMg= 2.24=48(g)
b) mMgO=40.2=80(g)
17 tháng 8 2021
Bài 14:
nCaCl2= 55,5/111= 0,5(mol)
a) PTHH: Ca +2 HCl -> CaCl2 + H2
Ta có: nH2=nCa=0,5(mol); nHCl=2.0,5=1(mol)
=> mHCl=1.36,5=36,5(g)
mCa= 40.0,5=20(g)
b) V(H2,đktc)=0,5.22,4=11,2(l)
câu 13, 14, 15 ạ giúp em với
7 tháng 1 2024
Câu 13:
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=10\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot10=6\cdot8=48\)
=>AH=48/10=4,8(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{6^2}{10}=3,6\left(cm\right)\\CH=\dfrac{8^2}{10}=6,4\left(cm\right)\end{matrix}\right.\)
Xét ΔHAB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM\cdot6=3,6^2\)
=>BM=2,16(cm)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\)
=>\(AN\cdot8=4,8^2\)
=>AN=2,88(cm)
ΔABN vuông tại A
=>\(AB^2+AN^2=BN^2\)
=>\(BN^2=2.88^2+6^2=44,2944\)
=>\(BN=\sqrt{44,2944}=\dfrac{6\sqrt{769}}{25}\left(cm\right)\)
Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>AH=MN=4,8(cm)
Xét ΔMBN có \(cosBMN=\dfrac{MB^2+MN^2-NB^2}{2\cdot MB\cdot MN}\)
\(=\dfrac{4,8^2+2,16^2-\dfrac{27684}{625}}{2\cdot4,8\cdot2,16}=\dfrac{-10368}{625}:\dfrac{2592}{125}=-\dfrac{4}{5}\)
=>\(sinBMN=\sqrt{1-\left(-\dfrac{4}{5}\right)^2}=\dfrac{3}{5}\)
Xét ΔBMN có \(\dfrac{NB}{sinBMN}=2R\)
=>\(2R=\dfrac{6\sqrt{769}}{25}:\dfrac{3}{5}=\dfrac{6\sqrt{769}}{25}\cdot\dfrac{5}{3}=\dfrac{2}{5}\sqrt{769}\)
=>\(R=\dfrac{\sqrt{769}}{5}\)
=>Chọn A
AH
Akai Haruma
Giáo viên
14 tháng 11 2023
Bài 11:
Gọi số học sinh giỏi 4 khối lần lượt là $a,b,c,d$ (em)
Theo bài ra ta có: $a+b+c-d=168$ và $\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}=\frac{a+b+c-d}{13+12+14-15}=\frac{168}{24}=7$
$\Rightarrow a=13.7=91; b=12.7=84; c=14.7=98; d=15.7=105$
AH
Akai Haruma
Giáo viên
14 tháng 11 2023
Bài 12:
Gọi số học sinh ba khối lần lượt là $a,b,c$ (học sinh).
Theo bài ra ta có: $\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$ và $a-b=50$
Áp dụng TCDTSBN:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{10-9}=\frac{50}{1}=50$
$\Rightarrow a=50.10=500; b=50.9=450; c=50.8=400$ (hs)
30 tháng 12 2023
Bài 14:
a: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
b: \(A=\dfrac{x}{2x+4}+\dfrac{3x+2}{x^2-4}\)
\(=\dfrac{x}{2\left(x+2\right)}+\dfrac{3x+2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x\left(x-2\right)+2\left(3x+2\right)}{2\left(x+2\right)\left(x-2\right)}\)
\(=\dfrac{x^2+4x+4}{2\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+2\right)^2}{2\left(x+2\right)\left(x-2\right)}=\dfrac{x+2}{2\left(x-2\right)}\)
c: Đặt B=2*A
\(\Leftrightarrow B=\dfrac{2\cdot\left(x+2\right)}{2\left(x-2\right)}=\dfrac{x+2}{x-2}\)
Để B là số nguyên thì \(x+2⋮x-2\)
=>\(x-2+4⋮x-2\)
=>\(4⋮x-2\)
=>\(x-2\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{3;1;4;0;6;-2\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;1;4;0;6\right\}\)
Bài 13:
1:
a: \(\dfrac{x^2-y^2}{x^2+xy}\cdot\dfrac{x+2y}{x-y}\)
\(=\dfrac{\left(x-y\right)\left(x+y\right)\left(x+2y\right)}{x\left(x+y\right)\left(x-y\right)}\)
\(=\dfrac{x+2y}{x}\)
b: \(x^2\cdot\left(2x-3y^2\right)-4xy\left(1-xy\right)-2x^3\)
\(=2x^3-3x^2y^2-4xy+4x^2y^2-2x^3\)
\(=x^2y^2-4xy\)
2:
\(f\left(x-2\right)=3\left(x-2\right)^2-4\)
\(=3\left(x^2-4x+4\right)-4\)
\(=3x^2-12x+8\)
\(f\left(4\right)=3\cdot4^2-4=48-4=44\)
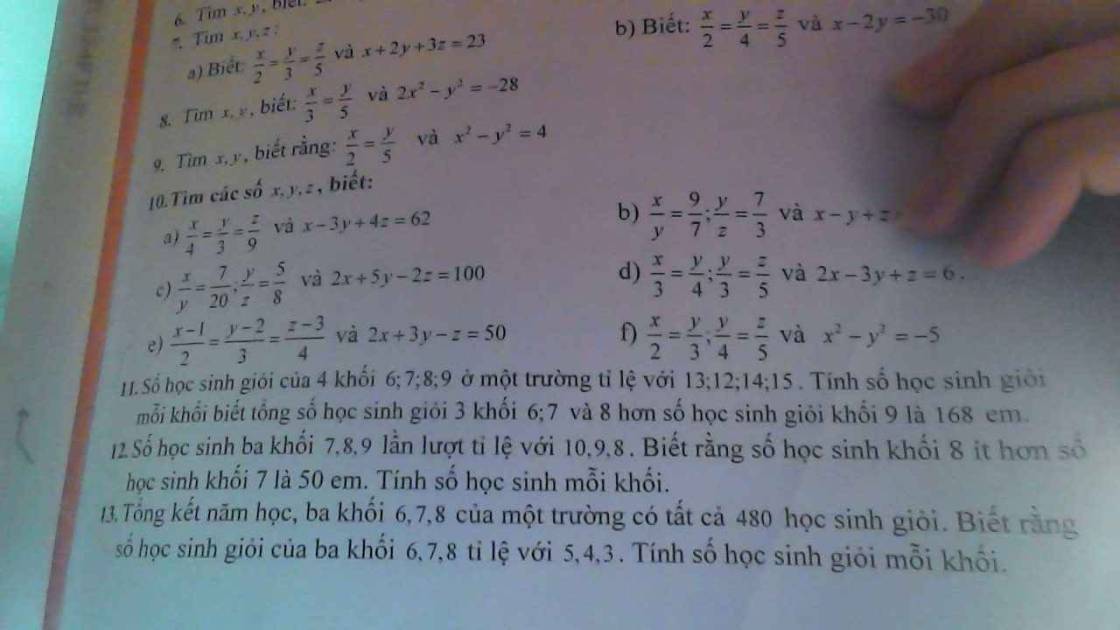
14.
\(\dfrac{1-cosa}{sina}=\dfrac{sina\left(1-cosa\right)}{sin^2a}=\dfrac{sina\left(1-cosa\right)}{1-cos^2a}=\dfrac{sin\left(1-cosa\right)}{\left(1-cosa\right)\left(1+cosa\right)}=\dfrac{sina}{1+cosa}\)
Câu b đề bài sai, đẳng thức đúng phải là: \(1+tan^2a=\dfrac{1}{cos^2a}\)
\(1+tan^2a=1+\dfrac{sin^2a}{cos^2a}=\dfrac{sin^2a+cos^2a}{cos^2a}=\dfrac{1}{cos^2a}\)
\(tan^2a-sin^2a=\dfrac{sin^2a}{cos^2a}-sin^2a=\dfrac{sin^2a}{cos^2a}\left(1-cos^2a\right)=\dfrac{sin^2a}{cos^2a}.sin^2a=tan^2a.sin^2a\)
\(\dfrac{sin^4a-cos^4a}{sina+cosa}=\dfrac{\left(sin^2a+cos^2a\right)\left(sin^2a-cos^2a\right)}{sina+cosa}=\dfrac{sin^2a-cos^2a}{sina+cosa}=\dfrac{\left(sina+cosa\right)\left(sina-cosa\right)}{sina+cosa}\)
\(=sina-cosa\)
13.
b. Chia cả tử và mẫu cho sinB:
\(N=\dfrac{\dfrac{4cosB}{sinB}+\dfrac{2sinB}{sinB}}{\dfrac{cossB}{sinB}-\dfrac{3sinB}{sinB}}=\dfrac{4cotB+2}{cotB-3}=\dfrac{4.\dfrac{3}{2}+2}{\dfrac{3}{2}-3}=-\dfrac{16}{3}\)
c. Chia cả tử và mẫu cho \(cos^3B\)
\(M=\dfrac{\dfrac{sin^3B}{cos^3B}-\dfrac{cos^3B}{cos^3B}}{\dfrac{sin^3B}{cos^3B}+\dfrac{cos^3B}{cos^3B}}=\dfrac{tan^3B-1}{tan^3B+1}=\dfrac{3^3-1}{3^3+1}=\dfrac{13}{14}\)