tìm các giá trị m sao cho phương trình : x4 + (1 - 2m)x2 + m2 - 1 = 0 : a) vô nghiệm ; b) có 2 nghiệm phân biệt ; c) có 4 nghiệm phân biệt .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Phương trình (1) vô nghiệm khi phương trình (2) có 2 nghiệm số âm hoặc vô nghiệm.
Nếu phương trình (2) có 2 nghiệm âm thì theo hệ thức Vi-ét ta có:
t 1 + t 2 = 13 > 0 vô lý
Vậy phương trình (1) vô nghiệm khi phương trình (2) vô nghiệm.
Suy ra: ∆ = 169 - 4m < 0 ⇔ m > 169/4}

Đk để pt trên có 2 nghiệm phân biệt x1,x2 : a>0 và denta>0
suy ra denta= (2m+1)^2-4.(m^2+1)>0
suy ra : m>3/4
Ta có P=x1x2/x1+x2=(m^2+1)/(2m+1)
Ta có: P∈Z
⇒4P∈Z
⇒(4m^2+4)/2m+1=(2m-1)+5/2m+1∈Z
⇒2m+1=Ư(5)={−5;−1;1;5}
⇒m={−3;−1;0;2}
Kết hợp đk m>3/4 ta được m=2

\(\Delta=\left(m+1\right)^2-4\left(m^2-2m+2\right)=-3m^2+10m-7\ge0\)
\(\Rightarrow1\le m\le\dfrac{7}{3}\)
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m^2-2m+2\end{matrix}\right.\)
\(P=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2\left(m^2-2m+2\right)\)
\(=-m^2+6m-3\)
\(=\left(-m^2+6m-\dfrac{77}{9}\right)+\dfrac{50}{9}\)
\(=\left(\dfrac{11}{3}-m\right)\left(m-\dfrac{7}{3}\right)+\dfrac{50}{9}\le\dfrac{50}{9}\)
\(P_{max}=\dfrac{50}{9}\) khi \(m=\dfrac{7}{3}\)

Để phương trình (1) có hai nghiệm trái dấu thì \(1\left(m^2+2m\right)< 0\)
\(\Leftrightarrow m^2+2m< 0\)
\(\Leftrightarrow m^2+2m+1< 1\)
\(\Leftrightarrow\left(m+1\right)^2< 1\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+1>-1\\m+1< 1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>-2\\m< 0\end{matrix}\right.\Leftrightarrow-2< m< 0\)

PT x 2 − 2 m + 1 x + m 2 − 1 = 0 ( 1 ) có 2 nghiệm phân biệt x 1 , x 2
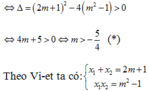
Theo Vi-et ta có: x 1 + x 2 = 2 m + 1 x 1 x 2 = m 2 − 1
Ta có: x 1 2 + x 2 2 + 8 x 1 x 2 = x 1 + x 2 2 + 6 x 1 x 2 = 2 m + 1 2 + 6 m 2 − 1
= 10 m 2 + 2 5 m + 1 25 − 27 5 = 10 m + 1 5 2 − 27 5
⇒ x 1 2 + x 2 2 + 8 x 1 x 2 ≥ − 27 5
Dấu ‘=’ xảy ra khi m = − 1 5 (thỏa mãn (*))
Vậy x 1 2 + x 2 2 + 8 x 1 x 2 đạt giá trị nhỏ nhất khi m = − 1 5
Đáp án cần chọn là: C

2 nghiệp pt phải:
(2m - 1)2-4(m2 - 1)≥0
Vì x1 là nghiệm nên
x21−(2m−1)x1+m2−1=0
<=> x12−(2m−1)x1+m2−1=0
<=>x12−2mx1+m2=x1+1
<=> 9m2=0 <=>m=0
#YQ

a: \(\Delta=\left(2m+2\right)^2-4\left(m^2-2m-3\right)\)
\(=4m^2+8m+4-4m^2+8m+12\)
=16m+16
Để phương trình luôn có nghiệm thì 16m+16>=0
hay m>=-1
b: Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2=28\)
\(\Leftrightarrow\left(2m+2\right)^2-3\left(m^2-2m-3\right)=28\)
\(\Leftrightarrow4m^2+8m+4-3m^2+6m+9=28\)
\(\Leftrightarrow m^2+14m-15=0\)
=>(m+15)(m-1)=0
=>m=1



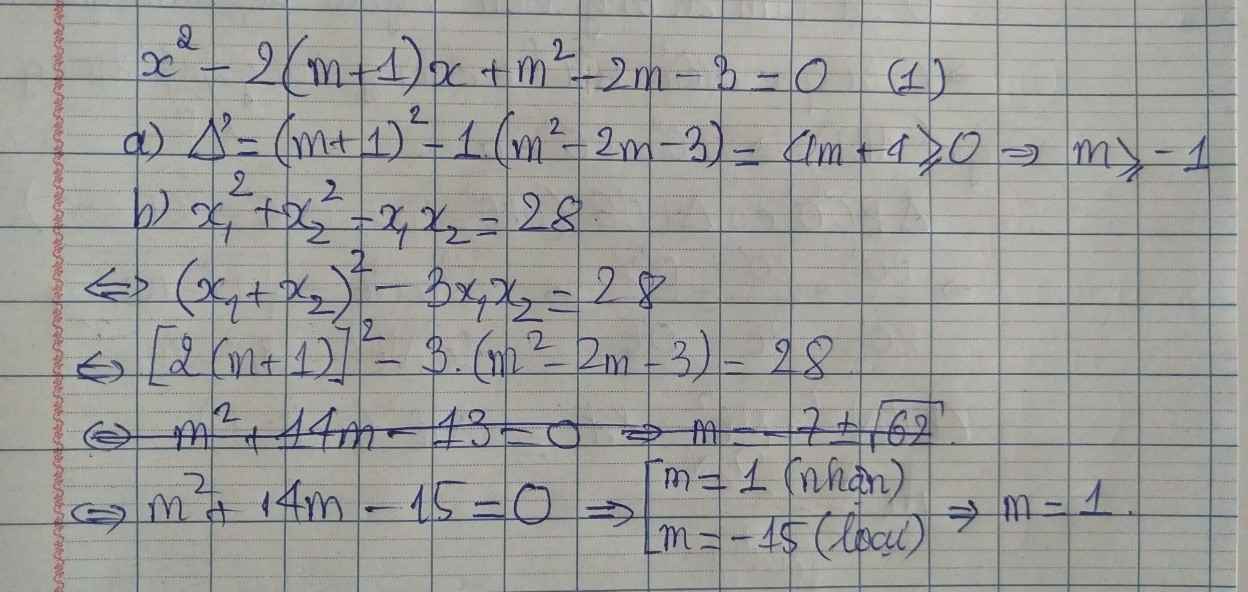
a) x4 + (1 - 2m)x2 + m2 - 1 = 0 (1)
Đặt t=x2 ta dc PT: t2+(1-2m)t+m2-1=0(2)
Để PT (1) thì PT(2) vô nghiệm:
Để PT(2) vô nghiệm thì: \(\Delta=\left(1-2m\right)^2-4.\left(m^2-1\right)<0\Leftrightarrow1-4m+4m^2-4m^2+4<0\)
<=>5-4m<0
<=>m>5/4
b)Để PT(1) có 2 nghiệm phân biệt thì PT(2) có duy nhất 1 nghiệm
Để PT(2) có duy nhất 1 nghiệm thì:
\(\Delta=5-4m=0\Leftrightarrow m=\frac{5}{4}\)
c)Để PT(1) có 4 nghiệm phân biệt thì PT(2) có 2 nghiệm phân biệt:
Để PT(2) có 2 nghiệm phân biệt thì:
\(\Delta=5-4m\ge0\Leftrightarrow m\le\frac{5}{4}\)
Mem đây ko rành lắm sai bỏ qua