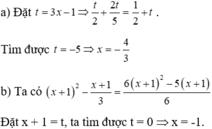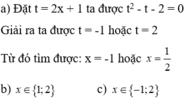giải phương trình sau : \(\sqrt{x^2+3x+12}\) = x2+3x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐK:x\(\ge\)0
Đặt t=x2+3x(t\(\ge\) 0)ta được:
\(\sqrt{t+12}=t\Leftrightarrow t^2=t+12\)
<=>t2-t-12=0
\(\Delta=49\Rightarrow\sqrt{\Delta}=7\)
\(\Delta>0,\text{phương trình có 2 nghiệm phân biệt}\)
\(t_1=4\left(thỏa\right);t_2=-3\left(loại\right)\)
t=4=>x2+3x=4
<=>x2+3x-4=0
\(\Delta=25\Rightarrow\sqrt{\Delta}=5;\Delta>0,pt\text{ có 2 nghiệm phân biệt:}\)
\(x_1=1\left(thỏa\right);x_2=-4\left(loại\right)\)
Vậy S={1}

ĐK: \(x\in R\)
\(pt\Leftrightarrow\sqrt{x^2+12}-4+3-\sqrt{x^2+5}+6-3x=0\)
\(\Leftrightarrow\dfrac{x^2-4}{\sqrt{x^2+12}+4}+\dfrac{4-x^2}{3+\sqrt{x^2+5}}+6-3x=0\)
\(\Leftrightarrow\left(\dfrac{x+2}{\sqrt{x^2+12}+4}-\dfrac{x+2}{3+\sqrt{x^2+5}}-3\right)\left(x-2\right)=0\left(1\right)\)
Từ phương trình suy ra \(3x-5=\sqrt{x^2+12}-\sqrt{x^2+5}>0\Rightarrow x>\dfrac{5}{3}\)
Ta có: \(\dfrac{x+2}{\sqrt{x^2+12}+4}-\dfrac{x+2}{3+\sqrt{x^2+5}}-3\)
\(=\left(\dfrac{1}{\sqrt{x^2+12}+4}-\dfrac{1}{3+\sqrt{x^2+5}}\right)\left(x+2\right)-3< 0\)
Khi đó \(\left(1\right)\Leftrightarrow x=2\left(tm\right)\)
Vậy phương trình đã cho có nghiệm \(x=2\)

Đặt m = x 2 +3x -1
Ta có: x 2 + 3 x - 1 2 +2( x 2 +3x -1) -8 =0 ⇔ m 2 +2m -8 =0
∆ ’ = 1 2 -1.(-8) =1 +8 =9 > 0
∆ ' = 9 =3
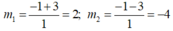
Với m = 2 thì : x 2 +3x - 1 = 2 ⇔ x 2 + 3x - 3 = 0
∆ ’ = 3 2 -4.1.(-3 )=9 +12=21 > 0
∆ ' = 21
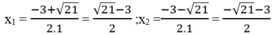
Với m = -4 ta có: x 2 +3x -1 = -4 ⇔ x 2 +3x +3 = 0
∆ = 3 2 -4.1.3=9 -12 = -3 < 0
Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm :
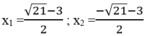

\(\Leftrightarrow x^2+1-\left(x+3\right)\sqrt{x^2+1}+3x=0\)
Đặt \(\sqrt{x^2+1}=t>0\)
\(\Rightarrow t^2-\left(x+3\right)t+3x=0\)
\(\Delta=\left(x+3\right)^2-12x=\left(x-3\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{x+3+x-3}{2}=x\\t=\dfrac{x+3-x+3}{2}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x^2+1}=x\left(x\ge0\right)\\\sqrt{x^2+1}=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=x^2\left(vô-nghiệm\right)\\x=\pm2\sqrt{2}\end{matrix}\right.\)
ĐK: Với mọi x thuộc R.
Ta có: \(x^2+3x+1=\left(x+3\right)\sqrt{x^2+1}\)
\(\Leftrightarrow\left(x^2+3x+1\right)^2=\left[\left(x+3\right)\sqrt{x^2+1}\right]^2\)
\(\Leftrightarrow x^4+6x^3+11x^2+6x+1=\left(x+3\right)^2\left(x^2+1\right)\)
\(\Leftrightarrow x^4+6x^3+11x^2+6x+1=x^4+6x^3+10x^2+6x+9\)
\(\Leftrightarrow x^2-8=0\)
\(\Leftrightarrow x^2=8\)
\(\left[{}\begin{matrix}x=2\sqrt{2}\\x=-2\sqrt{2}\end{matrix}\right.\)
Vậy....

\(\Leftrightarrow\left(x^2+2\right)\sqrt{x^2+x+1}-2\left(x^2+2\right)+x^3-x^2-5x+6=0\)
\(\Leftrightarrow\left(x^2+2\right)\left(\sqrt{x^2+x+1}-2\right)+\left(x-2\right)\left(x^2+x-3\right)=0\)
\(\Leftrightarrow\dfrac{\left(x^2+2\right)\left(x^2+x-3\right)}{\sqrt{x^2+x+1}+2}+\left(x-2\right)\left(x^2+x-3\right)=0\)
\(\Leftrightarrow\left(x^2+x-3\right)\left(\dfrac{x^2+2}{\sqrt{x^2+x+1}+2}+x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+x-3=0\Rightarrow x=...\\x^2+2=\left(2-x\right)\left(\sqrt{x^2+x+1}+2\right)\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^2+2x-2=\left(2-x\right)\sqrt{x^2+x+1}\)
Đặt \(\sqrt{x^2+x+1}=t>0\Rightarrow x^2=t^2-x-1\)
\(\Rightarrow t^2+x-3=\left(2-x\right)t\)
\(\Leftrightarrow t^2+\left(x-2\right)t+x-3=0\)
\(\Leftrightarrow t^2-1+\left(x-2\right)\left(t+1\right)=0\)
\(\Leftrightarrow\left(t+1\right)\left(t+x-3\right)=0\)
\(\Leftrightarrow t=3-x\)
\(\Leftrightarrow\sqrt{x^2+x+1}=3-x\) (\(x\le3\))
\(\Leftrightarrow x^2+x+1=x^2-6x+9\)
\(\Leftrightarrow x=\dfrac{8}{7}\)


1.\(A=\left(\sqrt{3}+1\right)\sqrt{\dfrac{14-6\sqrt{3}}{5+\sqrt{3}}}=\left(\sqrt{3}+1\right)\sqrt{\dfrac{\left(14-6\sqrt{3}\right)\left(5-\sqrt{3}\right)}{\left(5+\sqrt{3}\right)\left(5-\sqrt{3}\right)}}\)
\(=\left(\sqrt{3}+1\right)\sqrt{\dfrac{44\left(2-\sqrt{3}\right)}{22}}=\left(\sqrt{3}+1\right)\sqrt{4-2\sqrt{3}}=\left(\sqrt{3}+1\right)\sqrt{\left(\sqrt{3}-1\right)^2}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)=2\)
2.1.a) \(x^2=\left(x-1\right)\left(3x-2\right)\Leftrightarrow x^2=3x^2-5x+2\Leftrightarrow2x^2-5x+2=0\)
\(\Leftrightarrow\left(x-2\right)\left(2x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2}\end{matrix}\right.\)
b) \(9x^4+5x^2-4=0\Leftrightarrow9x^4+9x^2-4x^2-4=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-4\left(x^2+1\right)=0\Leftrightarrow\left(x^2+1\right)\left(9x^2-4\right)=0\)
mà \(x^2+1>0\Rightarrow9x^2=4\Rightarrow x^2=\dfrac{4}{9}\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
2) Gọi số xe lúc đầu của đội là a(xe) \(\left(a\in N,a>0\right)\)
Theo đề,ta có: \(\left(a-2\right)\left(\dfrac{120}{a}+3\right)=120\Leftrightarrow120+3a-\dfrac{240}{a}-6=120\)
\(\Leftrightarrow\dfrac{3a^2-6a-240}{a}=0\Rightarrow3a^2-6a-240=0\Rightarrow a^2-2a-80=0\)
\(\Leftrightarrow\left(a+8\right)\left(a-10\right)=0\) mà \(a>0\Rightarrow a=10\)