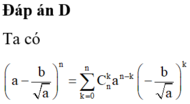Cho n thuộc Z* và a,b . Biết trong khai triển nhị thức niuton ((a/ cănb) + b) ^n có hạng từ chứa a^4b^9, tìm số hạng chứa tích a,b với số mũ bằng nhau.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 9 2017
Đáp án A
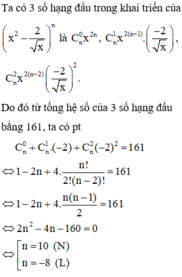
Vậy n = 10.
Ta có số hạng tổng quát trong khai triển trên là
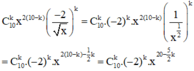
Vì a là hệ số của số hạng không chứa x trong khai triển nên ta cho
3 tháng 8 2018
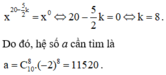
ta có : \(\left(2nx+\dfrac{1}{2nx^2}\right)^{3n}=\sum\limits^{3n}_{k=0}C^k_{3n}\left(2nx\right)^{3n-k}\left(\dfrac{1}{2nx^2}\right)^k\)
\(=\sum\limits^{3n}_{k=0}C^k_{3n}2^{3n-2k}\left(n\right)^{3n-2k}\left(x\right)^{3n-3k}\)
\(\Rightarrow\) tổng hệ số bằng : \(C^0_{3n}+C_{3n}^1+C^2_{3n}+...+C^{3n}_{3n}=64\)
\(\Leftrightarrow\left(1+1\right)^{3n}=64\Leftrightarrow2^{3n}=2^6\Rightarrow n=2\)
để có số hạng không chữa \(x\) không khai triển thì \(3n-3k=0\Leftrightarrow n=k\)
\(\Rightarrow\) hệ số của số hạng không chữa \(x\) là \(C^2_6.2^2.2^2=240\)
vậy ...........................................................................................................................
HZ
13 tháng 11 2019
Mysterious Person bn ơi cho mik hỏi chút nha , tại sao ở trên có
23n-2kn3n-2k mà ở dưới phần tổng hệ số í lại ko có ....Mong bn giúp mik ...