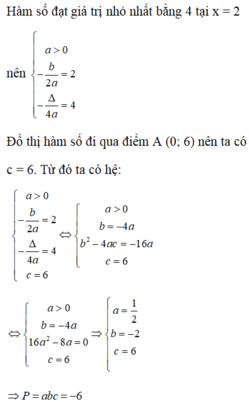tìm phương trình ( P ) ax2 + bx + c ( a khác 0 ) . Biết ( P) đi qua A ( 2 , 2 ) , B ( -2 , 10 ) và đạt giá trị nhỏ nhất là 12 .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án A
Phương trình đường thẳng đi qua hai điểm cực trị là
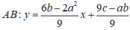
Vì I 0 ; 1 ∈ A B
![]()
Khi đó P = a b c + 2 a b + 3 c = 9 c 2 + 12 c - 18
⇒ P = 3 c + 2 2 - 22 ≥ - 22
Dấu “=” xảy ra ⇔ c = - 2 3

Chia cho X2 vì X=9 không là nghiệm của PT
Đặt t=X+\(\frac{1}{x}\)
=> t2+at+b-2=0
=>(t2-2)2=(at+b)2nhỏ hơn hoặc bằng (a2+b2)(1+t2)
=>a2+b2 lớn hơn hoặc bằng \(\frac{\left(t^2-2\right)^2}{t^2+1}\)lớn hơn hoặc bằng 0,8 dấu bằng khi..............

Gọi m là nghiệm chung của 2 phương trình thì ta có:
\(\hept{\begin{cases}m^2+am+6=0\\m^2+bm+12=0\end{cases}}\)
\(\Rightarrow2m^2+\left(a+b\right)m+18=0\)
Để phương trình có nghiệm thì
\(\Delta=\left(a+b\right)^2-144\ge0\)
\(\Leftrightarrow\left|a+b\right|\ge12\)
Ta lại có:
\(\left|a\right|+\left|b\right|\ge\left|a+b\right|\ge12\)
Tới đây thì đơn giản rồi nên b tự làm nhé.

muốn ít nhất có một phương trình có nghiệm thì tổng các đen ta >=0
nên đenta1+đenta2=b^2-4ac+c^2+4(a+c)a=b^2-4ac+c^2+4a^2+4ac>=0
vậy ......