gọi H là trực tâm của tam giác không vuông ABC . Chứng minh rằng bán kính các đường tròn ngoại tiếp các tam giác ABC , HBC . HCA . HAB bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



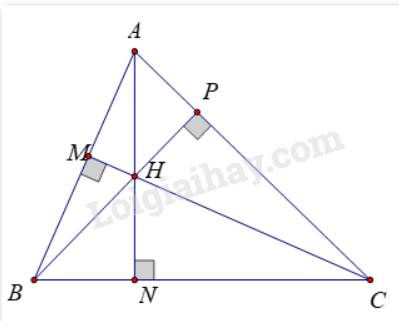
a)
Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC tại N, BH ⊥ AC tại P, CH ⊥ AB tại M
Trong ΔAHB, ta có:
HM ⊥ AB
BN ⊥ AH
Mà MH cắt BN tại C
=> C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
HP ⊥ AC
CN ⊥ AH
Mà HP cắt CN tại B
=> B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
HN ⊥ BC
BM ⊥ HC
Mà HN cắt BM tại A
=> A là trực tâm của tam giác HBC.

a/ Giả sử \(O_1\) là tâm của đường tròn ngoại tiếp tam giác HBC , thì \(O_1\) chính là ảnh của (O) qua phép đối xứng trục BC . Cho nên bán kính của chúng bằng nhau . Tương tự hai đường tròn ngoại tiếp của hai tam giác còn lại có bán kính bằng bán kính của (O) .
b/ Ta hoàn toàn chứng minh được \(O_1;O_2;O_3\) là các ảnh của O qua phép đối xứng trục BC,CA,AB . Vì vậy bán kính các đường tròn này bằng nhau . Mặt khác ta chứng minh tam giác ABC bằng tam giác
a/ Giả sử \(O_1\) là tâm của đường tròn ngoại tiếp tam giác HBC , thì \(O_1\) chính là ảnh của (O) qua phép đối xứng trục BC . Cho nên bán kính của chúng bằng nhau . Tương tự hai đường tròn ngoại tiếp của hai tam giác còn lại có bán kính bằng bán kính của (O) .
b/ Ta hoàn toàn chứng minh được \(O_1;O_2;O_3\) là các ảnh của O qua phép đối xứng trục BC,CA,AB . Vì vậy bán kính các đường tròn này bằng nhau . Mặt khác ta chứng minh tam giác ABC bằng tam giác \(O_1;O_2;O_3\)

a: Gọi D là giao của AC và HH'
=>HD=H'D
=>ΔAHH' cân tại A
=>góc AHH'=góc AHD=góc ACB
=>AH'CB là tứ giác nội tiếp

a . Gọi AH ∩ BC=D,BH ∩ AC=E,CH ∩ AB=F
\(\Rightarrow AD\perp BC,BE\perp AC,CF\perp AB\)
\(\Rightarrow\widehat{ADC}=\widehat{AFC}=90^0\) => ◊AFDC nội tiếp
\(\Rightarrow\widehat{DCF}=\widehat{DAF}\)
VÌ H đối xứng H' qua BC
\(\Rightarrow HH'\perp BC\Rightarrow A,H,,D,H'\)thẳng hàng
\(\Rightarrow\widehat{BAH'}=\widehat{DAF}=\widehat{FDC}=\widehat{HCB}\)
Lại có: H đối xứng với H' qua BC
\(\Rightarrow\widehat{BCH'}=\widehat{HCB}\)
\(\Rightarrow\widehat{BCH'}=\widehat{BAH'}\Rightarrow\)
\(\Rightarrow BC\perp AA'\Rightarrow A,H,D,H',A'\) thẳng hàng
Vì \(H,H'\) đối xứng qua BC , A,A' đối xứng qua BC
\(\Rightarrow\widehat{BHC}=\widehat{BH'C},\widehat{BAC}=\widehat{BA'C}\)
Lại có ◊ ABH'C nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{BH'C}=180^0\)
\(\Rightarrow\widehat{BA'C}+\widehat{BHC}=180^0\)
=> ◊ BHCA' nội tiếp
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp \(\Delta A'BC\)
Ta có : A , A' đối cứng qua BC
\(\Rightarrow A'B=AB,CA=CA'\Rightarrow\Delta ABC=\Delta A'BC\left(c.c.c\right)\)
=> Bán kính đường tròn ngoại tiếp \(\Delta A'BC\) bằng bán kính đường tròn ngoại tiếp ΔABC
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp ΔABC

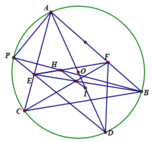
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.