Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu hoàn toàn tương tự như câu hỏi này mình đã trả lời ở đây, bạn tham khảo nhé:
/hoi-dap/question/15708.html
Hai giá trị của tần số góc cho cùng một giá trị của U C thõa mãn ω C 1 2 + ω C 2 2 = 2 ω C 2
Đáp án A
Số chỉ vôn kế đo được sẽ có sự chênh lệch so với số vôn ghi trên nhãn của nguồn điện (cụ thể là số chỉ vôn kế nhỏ hơn so với số chỉ trên nhãn).
Điều đó cho biết bên trong nguồn điện tồn tại điện trở trong.
Để làm bài này bạn cần áp dụng 1 số kết quả sau:
+ \(\omega=\omega_1\) thì \(u_{Cmax}\) \(\Rightarrow Z_C^2=Z^2+Z_L^2\) (*)
+ \(\omega = \omega_2\) thì \(u_{Lmax}\), khi đó hệ số công suất của mạch trong 2 trường hợp là như nhau.
Do vậy, ta tìm hệ số công suất của mạch trong trường hợp \(\omega=\omega_1\)
Ta có: \(U_C=3U\Rightarrow Z_C=3Z\)
(*) \(\Rightarrow (3Z)^2=Z^2+Z_L^2\)\(\Rightarrow Z_L=2\sqrt 2Z\)
Có: \(Z^2=R^2+(Z_L-Z_C)^2\) \(\Rightarrow Z^2=R^2+(2\sqrt 2 Z-3Z)^2\)
\(\Rightarrow Z^2=(17-12\sqrt 2)Z^2+R^2\)
\(\Rightarrow R=\sqrt{12\sqrt2 -16}.Z\)
\(\Rightarrow \cos\varphi=\dfrac{R}{Z}=\sqrt{12\sqrt2 -16}\)
Đáp án A
+ Khi V1max → mạch xảy ra cộng hưởng Z L = Z C 1 V 2 = U C = U Z L R với V1max = 2V2
→ ZL = 0,5R, để đơn giản ta chọn R = 1
→ ZL = 0,5 khi
V 2 m a x ⇒ V 2 = U c m a x = U R 2 + Z 2 L R = 5 2
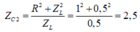
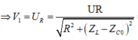
⇒ V 1 = 1 5
⇒ V 1 V 2 = 2 , 5
Bạn tham khảo một bài tương tự ở đây nhé Hỏi đáp - Trao đổi kiến thức Toán - Vật Lý - Hóa Học - Sinh Học - Học và thi online với HOC24
uMB vuông pha với uAB --> Mạch xảy ra cộng hưởng điện (do u cùng pha với i) \(\Rightarrow\omega_1=\frac{1}{\sqrt{LC}}\)
Số chỉ vôn kế: \(U_V=U_{RL}=\frac{U}{\sqrt{R^2+\left(Z_L-Z_C\right)^2}}.\sqrt{R^2+Z_L^2}\)
Để \(U_V\notin R\) thì \(Z_L=\left|Z_L-Z_C\right|\Rightarrow Z_C=2Z_L\Leftrightarrow\frac{1}{\omega_2C}=2\omega_2L\)
\(\Rightarrow\omega_2=\frac{1}{\sqrt{2LC}}=\frac{1}{\sqrt{2}}\omega_1\)
\(\Leftrightarrow\omega_1=\sqrt{2}\omega_2\)