Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(M=x^4+y^4+z^4=\left(x^4+\frac{1}{9}\right)+\left(y^4+\frac{1}{9}\right)+\left(z^4+\frac{1}{9}\right)-\frac{1}{3}\)
Áp dụng BĐT \(a^2+b^2\ge2ab\) ( "=" khi a=b ) , ta có :
\(M\ge\frac{2}{3}x^2+\frac{2}{3}y^2+\frac{2}{3}z^2-\frac{1}{3}\)
\(\Rightarrow M\ge\frac{1}{3}\left(2x^2+2y^2+2z^2\right)-\frac{1}{3}\)
\(\Rightarrow M\ge\frac{1}{3}\left[\left(x^2+y^2\right)+\left(y^2+z^2\right)+\left(x^2+z^2\right)\right]-\frac{1}{3}\)
\(\Rightarrow M\ge\frac{2}{3}.\left(xy+yz+xz\right)-\frac{1}{3}=\frac{2}{3}-\frac{1}{3}=\frac{1}{3}\) ( Vì xy+yz+xz=1 )
Dấu "=" xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}\)
Vậy \(GTNN_M=\frac{1}{3}\) khi \(x=y=z=\frac{1}{\sqrt{3}}\)
( Ko bít đúng Ko ) :)

\(A^2=\left(x-y\right)^2=\left(1.x+\dfrac{1}{2}.\left(-2y\right)\right)^2\le\left(1+\dfrac{1}{4}\right)\left(x^2+4y^2\right)=\dfrac{5}{4}\)
\(\Rightarrow A\le\dfrac{\sqrt{5}}{2}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(-\dfrac{2\sqrt{5}}{5};\dfrac{\sqrt{5}}{10}\right);\left(\dfrac{2\sqrt{5}}{5};-\dfrac{\sqrt{5}}{10}\right)\)

Lời giải:
Áp dụng BĐT AM-GM:
\(\frac{x^2}{2}+8y^2\geq 4xy\)
\(\frac{x^2}{2}+8z^2\geq 4xz\)
\(2(y^2+z^2)\geq 4yz\)
\(4y^2+1\geq 4y\)
\(4y+2\geq 4\sqrt{2y}\)
Cộng theo vế các BĐT trên ta có:
\(P+3\geq 4(xy+yz+xz)=\frac{9}{4}.4=9\Rightarrow P\geq 6\)
Vậy $P_{\min}=6$. Giá trị này đạt tại $(x,y,z)=(2,\frac{1}{2}, \frac{1}{2})$
Mấy bài như này có cách làm chung không ạ?Hay phải tự nháp...

\(P=\dfrac{1}{ab}+\dfrac{1}{bc}+\dfrac{1}{ac}+\dfrac{1}{a^2+b^2+c^2}\ge\dfrac{\left(1+1+1\right)^2}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\) (BĐT Cauchy Schwarz)
\(=\dfrac{9}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}\)
\(=\dfrac{1}{ab+bc+ca}+\dfrac{1}{ab+bc+ca}+\dfrac{1}{a^2+b^2+c^2}+\dfrac{7}{ab+bc+ca}\)
\(\ge\dfrac{\left(1+1+1\right)^2}{a^2+b^2+c^2+2ab+2ac+2bc}+\dfrac{7}{ab+bc+ca}\)
\(=\dfrac{9}{\left(a+b+c\right)^2}+\dfrac{7}{ab+bc+ca}\)
Ta có: \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}=\dfrac{1}{3}\) .Thế vào biểu thức
\(\Rightarrow P\ge9+\dfrac{7}{\dfrac{1}{3}}=9+21=30\)
\(\Rightarrow P_{min}=30\) khi \(a=b=c=\dfrac{1}{3}\)

Áp dụng BĐT Cô - si cho 2 số \(\frac{xy}{z};\frac{yz}{x}\)dương ta có: \(\frac{xy}{z}+\frac{yz}{x}\ge2\sqrt{\frac{xy}{z}.\frac{yz}{x}}=2\sqrt{y^2}=2y\)(1)
Tương tự. \(\frac{yz}{x}+\frac{zx}{y}\ge2\sqrt{\frac{yz}{x}.\frac{zx}{y}}=2\sqrt{z^2}=2z\) (2);
\(\frac{xy}{z}+\frac{zx}{y}\ge2\sqrt{\frac{xy}{z}.\frac{zx}{y}}=2\sqrt{x^2}=2x\)(3)
Cộng từng vế của (1)(2)(3) ta được \(2.\left(\frac{xy}{z}+\frac{yz}{x}+\frac{zx}{y}\right)\ge2\left(x+y+z\right)=2\Rightarrow P\ge1\)
Vậy Min P = 1 tại x= y = z = 1/3

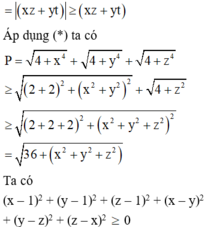
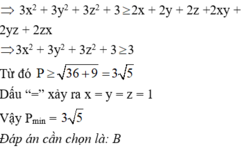
\(T=x^4+y^4+z^4\)
áp dụng bđt bunhia cốp -xki với bộ số \(\left(x^2,y^2,z^2\right);\left(1,1,1\right)\)
\(\left(\left[x^2\right]^2+\left[y^2\right]^2+\left[z^2\right]^2\right)\left(1^2+1^2+1^2\right)\ge\left(x^2+y^2+z^2\right)^2\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(x^2+y^2+z^2\right)^2}{3}\)
\(\left(x^4+y^4+z^4\right)\ge\frac{\left(2xy+2yz+2xz\right)^2}{3}\)(bđt tương đương)
\(\left(x^4+y^4+z^4\right)\ge\frac{4}{3}\)
dấu "=" xảy rakhi và chỉ khi
\(\hept{\begin{cases}\frac{x^2}{1}=\frac{y^2}{1}=\frac{z^2}{1}\\x=y=z=1\end{cases}< =>\frac{1^2}{1}=\frac{1^2}{1}=\frac{1^2}{1}}\)(luôn đúng)
vậy dấu "=" có xảy ra
\(< =>MIN:T=\frac{4}{3}\)
sửa dòng 3 dưới lên
\(T\ge\frac{\left(xy+yz+xz\right)^2}{3}=\frac{1}{3}\)
Dấu ''='' xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}\)
Vậy GTNN T là 1/3 khi \(x=y=z=\frac{\sqrt{3}}{3}\)