Cho hàm số \(y=\frac{3\left(x+1\right)}{x-2}\)(C)
Tìm tất cả các điểm trên (C) có tọa độ nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 1 2018
Để tìm trên (C) các điểm có tọa độ nguyên ta có:
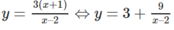
Điều kiện cần và đủ để M(x, y) ∈ (C) có tọa độ nguyên là:
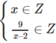
tức (x – 2) là ước của 9.
Khi đó, x – 2 nhận các giá trị -1; 1; -3; 3; -9; 9 hay x nhận các giá trị 1; 3; -1; 5; -7; 11.
Do đó, ta có 6 điểm trên (C) có tọa độ nguyên là: (1;-6), (3;12), (-1;0), (5;6), (-7;2), (11;4).
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a)
+) Thay tọa độ \(\left( { - 1; - 2} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 2 = - 2.{\left( { - 1} \right)^2}\)(Đúng)
=> \(\left( { - 1; - 2} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;0} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(0 = - {2.0^2}\)(Đúng)
=> \(\left( {0;0} \right)\) thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {0;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.0^2} \Leftrightarrow 1 = 0\)(Vô lí)
=> \(\left( {0;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
+) Thay tọa độ \(\left( {2021;1} \right)\) vào hàm số \(y = - 2{x^2}\) ta được:
\(1 = - {2.2021^2}\)(Vô lí)
=> \(\left( {2021;1} \right)\) không thuộc đồ thị hàm số \(y = - 2{x^2}\).
b)
+) Thay \(x = - 2\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( { - 2} \right)^2} = - 8\)
+) Thay \(x = 3\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - {2.3^2} = - 18\)
+) Thay \(x = 10\) vào hàm số \(y = - 2{x^2}\) ta được:
\(y = - 2.{\left( {10} \right)^2} = - 200\)
c) Thay \(y = - 18\) vào hàm số \(y = - 2{x^2}\) ta được:
\( - 18 = - 2{x^2} \Leftrightarrow {x^2} = 9 \Leftrightarrow x = \pm 3\)
Vậy các điểm có tọa độ (3;-18) và (-3;-18) thuộc đồ thị hàm số có tung độ bằng -18.
29 tháng 4 2016
a) Ta có : \(y'=3x^2+2\left(m-1\right)x+m\left(m-3\right)\)
Hàm số (1) có cực đại và cực tiểu nằm 2 phía đối với trục tung <=> phương trình : \(3x^2+2\left(m-1\right)x+m\left(m-3\right)=0\) có 2 nghiệm phân biệt trái dấu
\(\Leftrightarrow P< 0\Leftrightarrow m\left(m-3\right)< 0\Leftrightarrow0< m< 3\)
Vậy \(0< m< 3\) là giá trị cần tìm
b) Khi m = 1 ta có : \(y=x^3-2x\).
Gọi \(M\left(a;a^3-2a\right)\in\left(C\right),a\ne0\)
Ta có \(y'=3x^2-2\) nên hệ số góc của \(\Delta\) là \(y'\left(a\right)=3a^2-2\)
Ta có \(\overrightarrow{OM}\left(a;a^3-2a\right)\) nên hệ số góc đường thẳng OM là \(k=a^2-2\)
Do đó : \(\Delta\perp OM\Leftrightarrow y'_a.k=-1\)
\(\Leftrightarrow\left(3a^2-2\right)\left(a^2-2\right)=-1\Leftrightarrow3a^4-8a^2+5=0\)
\(M_1\left(1;-1\right);M_1\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a^2=1\\a^2=\frac{5}{3}\end{array}\right.\) \(\Leftrightarrow\left[\begin{array}{nghiempt}a=\pm1\\a=\pm\frac{\sqrt{5}}{3}\end{array}\right.\)(Thỏa mãn)
Suy ra có 4 điểm thỏa mãn đề bài :\(M_1\left(1;-1\right);M_2\left(-1;1\right);M_3\left(-\frac{\sqrt{15}}{3};\frac{\sqrt{15}}{9}\right);M_4\left(\frac{\sqrt{15}}{3};-\frac{\sqrt{15}}{9}\right)\)
5 tháng 2 2022
a: ĐKXĐ: \(\left\{{}\begin{matrix}-2< =x< =2\\x< >0\end{matrix}\right.\)
c: \(f\left(-x\right)=\dfrac{\sqrt{2-\left(-x\right)}-\sqrt{2+\left(-x\right)}}{-x}=\dfrac{\sqrt{2+x}-\sqrt{2-x}}{-x}=\dfrac{\sqrt{2-x}-\sqrt{2+x}}{x}=f\left(x\right)\)
12 tháng 9 2023
a)
- Với \(x = - 2 \Rightarrow f\left( { - 2} \right) = - 2;g\left( { - 2} \right) = - 2 + 3 = 1\);
- Với \(x = - 1 \Rightarrow f\left( { - 1} \right) = - 1;g\left( { - 1} \right) = - 1 + 3 = 2\);
- Với \(x = 0 \Rightarrow f\left( 0 \right) = 0;g\left( 0 \right) = 0 + 3 = 3\);
- Với \(x = 1 \Rightarrow f\left( 1 \right) = 1;g\left( 1 \right) = 1 + 3 = 4\);
- Với \(x = 2 \Rightarrow f\left( 2 \right) = 2;g\left( 2 \right) = 2 + 3 = 5\);
Ta có bảng sau:
\(x\) | –2 | –1 | 0 | 1 | 2 |
\(y = f\left( x \right) = x\) | –2 | –1 | 0 | 1 | 2 |
\(y = g\left( x \right) = x + 3\) | 1 | 2 | 3 | 4 | 5 |
b)
- Vẽ đồ thị hàm số \(y = f\left( x \right) = x\)
Cho \(x = 1 \Rightarrow y = f\left( x \right) = 1\). Ta vẽ điểm \(A\left( {1;1} \right)\)
Đồ thị hàm số \(y = x\) là đường thẳng đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {1;1} \right)\).
- Các điểm có tọa độ thỏa mãn hàm số \(y = g\left( x \right)\) trong bảng trên là \(B\left( { - 2;1} \right);C\left( { - 1;2} \right);D\left( {0;3} \right);E\left( {1;4} \right);F\left( {2;5} \right)\).
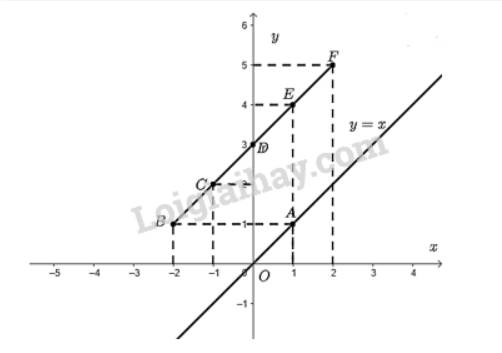
c) Ta đặt thước thẳng kiểm tra thì thấy các điểm thuộc đồ thị hàm số \(y = g\left( x \right) = x = 3\) thẳng hàng với nhau.
Dự đoán cách vẽ đồ thị hàm số \(y = g\left( x \right)\):
Bước 1: Chọn hai điểm \(A;B\) phân biệt thuộc đồ thị hàm số \(y = g\left( x \right)\).
Bước 2: Vẽ đường thẳng đi qua hai điểm \(A;B\).
Đồ thị hàm số \(y = g\left( x \right)\) là đường thẳng đi qua hai điểm \(A;B\).
ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....