Vận tốc của một vật dao động điều hoà khi đi quan vị trí cân bằng là 1cm/s và gia tốc của vật khi ở vị trí biên là 1,57cm/s2. Chu kì dao động của vật là
A.3,14s.
B.6,28s.
C.4s.
D.2s.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vận tốc của vật tại vị trí cân bằng v = vmax, gia tốc của vật tại biên a = amax.
Ta có
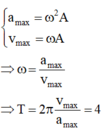
Đáp án C

ü Đáp án C
+ Vận tốc của vật tại vị trí cân bằng v = vmax, gia tốc của vật tại biên a = amax.
Ta có a m a x = ω 2 A v m a x = ω A ⇒ ω = a m a x v m a x ⇒ T = 2 π v m a x a m a x = 4

Hướng dẫn:
+ Khi qua VTCB vật đạt vận tốc cực đại: \(v_{max}=\omega.A=62,8(cm/s)=20\pi(cm/s)\)
+ Khi vật ở biên thì gia tốc cực đại: \(a_{max}=\omega^2.A=200cm/s^2\)
Giải hệ pt trên ta tìm đc \(\omega=\pi(rad/s) \); \(A=20cm\)

Bạn xem lại giả thiết xem có thừa thiếu chỗ nào không nhé, giả thiết bài này khó hiểu quá.

Đáp án B
+ Phát biểu đúng là:
(e) cứ mỗi chu kỳ dao động, có 4 thời điểm thế năng và động năng của vật bằng nhau.
(g) gia tốc đạt giá trị cực tiểu khi vật ở ly độ cực đại.

+ Phát biểu đúng là:
(e) cứ mỗi chu kỳ dao động, có 4 thời điểm thế năng và động năng của vật bằng nhau.
(g) gia tốc đạt giá trị cực tiểu khi vật ở ly độ cực đại.
Đáp án B
+ Khi qua VTCB, vận tốc đạt cực đại \(\Rightarrow v_{max}=\omega A = 1 \ (cm/s)\) (1)
+ Khi ở biên, gia tốc đạt cực đại \(\Rightarrow a_{max}=\omega^2 A = 1,57 \ (cm/s^2)\) (2)
Từ (1) và (2): \(\omega = 1,57 = \frac{\pi}{2} \ (rad/s)\)
Vậy chu kì: T = 4s
tìm A kiểu j vậy