CMR:
\(y=\frac{2x^2+3x}{2x+1}\) đồng biến trên mỗi khoảng xác định của nó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 5 2019
Chọn B.
Hàm số (I): 
, ∀x ∈ D = R \ {-1} nên hàm số đồng biến trên từng khoảng xác định của nó.
Hàm số (II): y’ = -4x3 + 2x. y' = 0 <=> - 4x3 + 2x = 0 <=>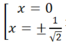 
nên hàm số không đồng biến trên khoảng xác định của nó.
Hàm số (III): y’ = 3x2 – 3.
y’ = 0 <=> 3x2 – 3 = 0 <=> x = ±1 nên hàm số không đồng biến trên khoảng xác định của nó.
CM
4 tháng 12 2019
Tập xác định: D = R ∖ { 1 }
· y ' = m x 2 + 2 m x + 1 x + 1 2
· Hàm số luôn đồng biến trên từng khoảng xác định của nó khi và chỉ khi y ' > 0; ∀ x ≠ 1
· Xét m = 0, ta có y ' = 1 x + 1 2 > 0 ; ∀ x ≠ 1 (tm).
· Xét m ≠ 0 .Yêu cầu bài toán
⇔ ∆ ' = m 2 - m ≤ 0 m > 0 ⇔ 0 ≤ m ≤ 1 m > 0 ⇔ 0 < m ≤ 1
Kết luận: 0 ≤ m ≤ 1
Đáp án B
CM
2 tháng 7 2018
Chọn D.
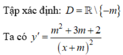
Để hàm số đã cho nghịch biến trên khoảng xác định:
⇔ y' < 0, ∀ x ∈ D ⇔ m2 + 3m + 2 < 0 ⇔ -2 < m < -1
Vậy không có số nguyên m nào thuộc khoảng (-2;-1).
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
CM
19 tháng 5 2017
Đáp án A
T X D : D = ℝ \ 1
Ta có: y = m x 2 − m + 2 x + m 2 − 2 m + 2 x − 1 = m x − 2 + m 2 − 2 m x − 1 ⇒ y ' = m − m 2 − 2 m x − 1 2
hàm số luôn đồng biến trên tập xác định của nó khi y ' ≥ 0 ∀ x ∈ D (dấu bằng xảy ra tại hữu hạn điểm)
⇔ m − m 2 − 2 m x − 1 2 ≥ 0 ∀ x ∈ D ⇔ x x − 1 2 ≥ m 2 − 2 m ∀ x ∈ D
Với m = 0 ⇒ y ' = 0 ∀ x ∈ D (không thỏa mãn dấu bằng xảy ra tại hữu hạn điểm)
Khi đó hàm số luôn đồng biến trên tập xác định m > 0 m 2 − 2 m ≤ 0 ⇔ 0 < m ≤ 2
điều kiện để hàm số đơn điệu trên một khoảng là
a, nếu f'(x)>0 với mọi x thuộc khoảng đó thì hàm số đồng biến trên khoảng đó
b, nếu f'(x)<0 với mọi x thuộc khoảng đó thì hàm số nghịch biến trên khoảng đó
c, nếu f'(x)=0 với mọi x thuộc khoảng đó thì hàm số không đổi trên khoảng đó
áp dụng vào bài trên ta có
f'(x)=\(\frac{4x^2+4x+3}{\left(2x+1\right)^2}>0\) với mọi x\(\pm\)\(\frac{-1}{2}\)
vậy hàm số đồng biến trên \(R\backslash\left\{\frac{-1}{2}\right\}\)