Thực hiện giao thoa cơ với hai nguồn \(S_1,S_2\) ngược pha, cùng biên độ 1cm, bước sóng \(\lambda\) = 20cm thì điểm M cách S1 50cm và cách S2 10cm có biên độ
A. 0.
B. \(\sqrt{2}\)cm.
C.\(\sqrt{2}/2\) cm.
D.2cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
9 tháng 8 2018
Đáp án: B
HD Giải: A M = 2 . 1 . cos π ( 50 - 10 ) 20 = 2 c m
VT
29 tháng 10 2018
Đáp án C
Vì 2 nguồn cùng biên độ, cùng pha nên biên độ tại điểm M là: A = 2 a cos π d 1 - d 2 λ = 2 c m
VT
15 tháng 12 2018
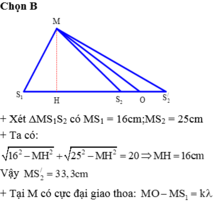
+ Vì O nằm trên khoảng S 2 S 2 '
M S 2 - M S 1 < k λ < M S 2 ' - M S 1 ⇒ 25 - 16 < 3 k < 33 , 3 - 16 ⇒ 3 < k < 5 , 7
Có hai giá trị k nguyên ứng với hai lần nguồn tạo ra tại M dao động với biên độ cực đại
VT
4 tháng 11 2019
Đáp án A.
Lời giải chi tiết:
Độ lệch pha của điểm M với hai nguồn là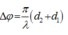 
Điều kiện để M lệch pha π 2 so với nguồn:
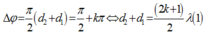
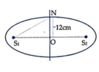
Vậy quỹ tích các điểm lệch pha π 2 so với nguồn là đường elip thỏa mãn đều kiện (1) nhận S1 và S2 làm tiêu điểm.
+ Điều kiện để các đường elip này nằm trong (E) là:
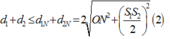
+ Mặt khác tổng các cạnh trong một tam giác lớn hơn cạnh còn lại nên
Kết hợp (1), (2) và (3) ta có:
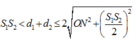
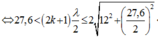
Vậy có 2 đường elip nằm trong € mà các điểm trên đó lệch pha π 2 so với nguồn.
+ Số điểm giao động với biên độ cực đại trên đoạn thẳng nối hai nguồn:
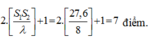
+ Vì 1 đường cực đại cắt elip tại 2 điểm nên trên 1 đường elip có 14 điểm dao động với biên độ cực đại.
Vậy trên 2 đường elip có 28 điểm dao động với biên độ cực đại và lệch pha π 2 số với nguồn.
Hai nguồn ngược pha, cùng biên độ => \(\triangle\varphi = \pi\)
Biên độ tại điểm M là
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\frac{\pi}{2}| = 0.\)