Một con lắc lx treo thẳg đứg .kích thík cho con lắc lx dao độg theo pkươg thẳg đứg . T=0,4s và A=8cm . Chọn trục x'x thẳg đứg theo chjều dươg hướg xuốg, gốc tọa độ tạj VTCB ,gốc thờj jan t=0 khj vật wa VTCB theo chjều dươg. Lấy gja tốc rơj tự do g=10m/s^2 và pi^2=10. Thờj jan ngắn nhất kể từ khj t=0 đến khj lực đàn hồj của lò xo có độ lớn cực tjểu bằg bao nhjêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác:

Đáp án D

Đáp án D
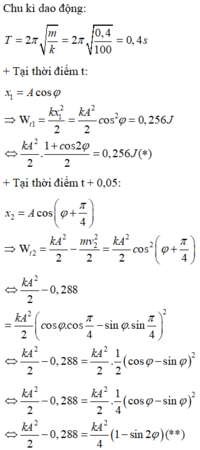
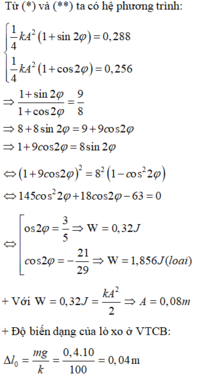
+ Thời gian lò xo giãn trong một chu kì được biểu diễn trên đường tròn lượng giác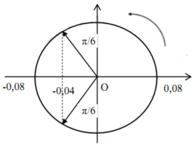
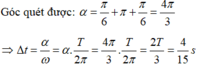

Do \(\alpha_0=8^0\) nên đây là dao động điều hòa, ta tính toán giống như một dao động điều hòa thôi.
Tại vị trí \(W_đ=W_t\)
\(\Rightarrow W=W_đ+W_t=2W_đ\)
\(\Rightarrow v_{max}^2=2.v^2\)
\(\Rightarrow v=\dfrac{v_{max}}{\sqrt 2}=\dfrac{\omega.A}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\sqrt{\dfrac{g}{\ell}}.\alpha_0.\ell}{\sqrt 2}=\dfrac{\alpha_0.\sqrt{g.\ell}}{\sqrt 2}\)
\(\Rightarrow v=\dfrac{\dfrac{8.\pi}{180}.\sqrt{10.1}}{\sqrt 2}\approx0,31(m/s)\)

Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
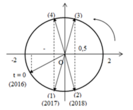
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
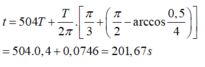
Đáp án C

Đáp án C
Chu kì dao động: T = 2π/ω = 2π/5π = 0,4s
Thời điểm t = 0 và thời điểm độ lớn lực đàn hồi bằng 0,5N được biểu diễn trên đường tròn lượng giác:
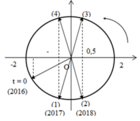
Một chu kì có 4 lần độ lớn lực đàn hồi bằng 0,5N
Sau 504T độ lớn lực đàn hồi bằng 0,5N lần thứ 2016
=> Lực đàn hồi có độ lớn bằng 0,5N lần thứ 2018 vào thời điểm:
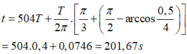

\(b,\text{PT giao Ox và Oy: }\\ y=0\Leftrightarrow x=\dfrac{3}{2}\Leftrightarrow A\left(\dfrac{3}{2};0\right)\Leftrightarrow OA=\dfrac{3}{2}\\ x=0\Leftrightarrow y=3\Leftrightarrow B\left(0;3\right)\Leftrightarrow OB=3\\ \Leftrightarrow S_{OAB}=\dfrac{1}{2}OA\cdot OB=\dfrac{1}{2}\cdot\dfrac{3}{2}\cdot3=\dfrac{9}{4}\left(cm^2\right)\\ c,C_1:\text{Áp dụng Pytago: }AB=\sqrt{OA^2+OB^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\\ C_2:AB=\sqrt{\left(x_A-x_B\right)^2+\left(y_A-y_B\right)^2}=\sqrt{\left(\dfrac{3}{2}-0\right)^2+\left(0-3\right)^2}=\dfrac{3\sqrt{5}}{2}\left(cm\right)\)

+ Phương trình dao động của hai con lắc lò xo
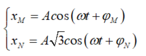
Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là:
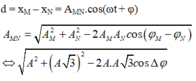
Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A
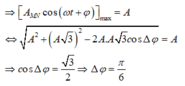
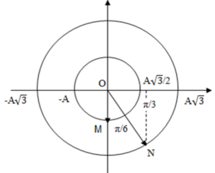
Động năng của con lắc M cực đại W đ m = k A 2 2 = 0 , 12 J khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).
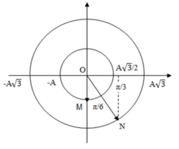
+ Từ đường tròn lượng giác xác định được

Đáp án D

Đáp án A
+ Phương trình dao động của hai con lắc lò xo:
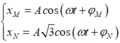
+ Khoảng cách giữa hai vật nặng của hai con lắc lò xo tại thời điểm t là:
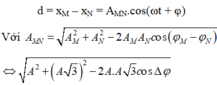
+ Trong quá trình dao động, độ chênh lệch độ cao lớn nhất của hai vật là A:
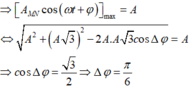
+ Động năng của con lắc M cực đại W dM = kA 2 2 = 0 , 12 J khi vật M ở VTCB. Khi đó ta biểu diễn được vị trí của vật N được biểu diễn trên đường tròn lượng giác (M và N lệch pha nhau góc π/6).
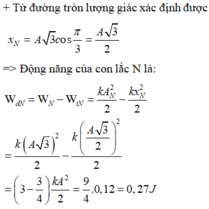

Giải thích: Đáp án C
Phương pháp:
Lưc̣ đàn hồi = (đô ̣cứng).(đô ̣biến dang̣)
Sử dung̣ đường tròn lượng giác
Cách giải:
Trục Ox thẳng đứng hướng xuống, gốc O trùng VTCB
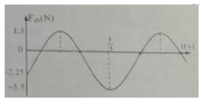
Từ đồ thị ta có:
Lực đàn hồi cực tiểu: Fmin = 0N
Lực đàn hồi giãn cực đại: ![]()
Lực đàn hồi nén cực đại: 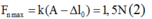
Từ (1) và (2) ![]()
Tại t = 0: ![]()
Ngay sau thời điểm t = 0 thì lực đàn hồi có độ lớn giảm => vật đang đi về phía VTCB
=> Tại t = 0: x = 5 và vật đi về phía vị trí cân bằng. Biểu diễn trên đường tròn lượng giác ta có:
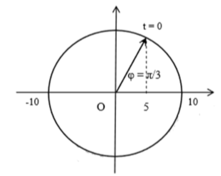
=> Pha ban đầu: φ=π/3
=> Phương trình dao động của vật: x = 10cos(5 πt + π/3)
\(T=2\pi\sqrt{\frac{\Delta l_0}{g}}\Rightarrow\Delta l_0=\frac{T^2}{4\pi^2}g=4cm\)
Như vậy, lực đàn hồi cực tiểu tại vị trí lò xo không biến dạng, có li độ là -4cm.
Bài toán trở thành tính thời gian ngắn nhất vật đi từ VTCB theo chiều dương đến li độ -4cm.
Vẽ véc tơ quay, ta tìm đc thời gian: \(\Delta t=\frac{180+30}{360}.T=\frac{7}{12}.0,4=\frac{7}{30}s\)
do đọc sách không đúng cách không giữ đúng khoảng cách