Tại hai điểm S1, S2 cách nhau 3 cm trên mặt nước đặt hai nguồn kết hợp phát sóng ngang với cùng phương trình \(u=2\cos(100 \pi t)mm,\) t tính bằng giây. Tốc độ truyền sóng trong nước là 20 cm/s. Coi biên độ sóng không đổi khi truyền đi. Phương trình sóng tại điểm M nằm trên mặt nước với S1M = 5,3cm và S2M = 4,8cm là
A. \(u=4\cos(100\pi-0,5\pi)mm.\)
B. \(u=2\cos(100\pi+0,5\pi)mm.\)
C. \(u=2\sqrt{2}\cos(100\pi-24,25\pi)mm.\)
D.\(u=2\sqrt{2}\cos(100\pi-25,25\pi)mm.\)





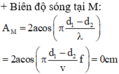
\(\lambda = v/f=20/50=0.4cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{4,8-5,3}{0,4}-\frac{0}{2\pi})|=|2a\cos\frac{-5\pi}{4}|=\sqrt{2}a = 2\sqrt{2}\)
\( u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})=2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4}+\frac{0}{2}) = 2\sqrt{2}\cos(40 \pi t - \pi\frac{5,3+4,8}{0,4})\\ = 2\sqrt{2}\cos(40 \pi t - 25,25\pi)mm.\)