Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc thế năng tính tại vị trí cân bằng. Từ thời điểm \(t_1=0\) đến \(t_2= \frac {\pi} {48}s\), động năng của con lắc tăng từ 0,096J đến giá trị cực đại rồi giảm về 0,064J. ở thời điểm \(t_2\), thế năng của con lắc bằng 0,096J. Biên độ dao động của con lắc là:A.5,7 cm. B.7,0 cm. C.8,0...
Đọc tiếp
Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ khối lượng 100g đang dao động điều hòa theo phương ngang, mốc thế năng tính tại vị trí cân bằng. Từ thời điểm \(t_1=0\) đến \(t_2= \frac {\pi} {48}s\), động năng của con lắc tăng từ 0,096J đến giá trị cực đại rồi giảm về 0,064J. ở thời điểm \(t_2\), thế năng của con lắc bằng 0,096J. Biên độ dao động của con lắc là:
A.5,7 cm.
B.7,0 cm.
C.8,0 cm.
D.3,6 cm.
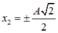
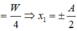
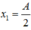
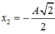
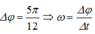
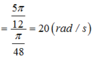
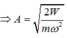
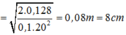
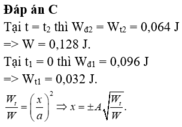
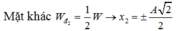
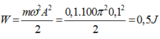
Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
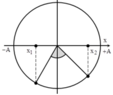
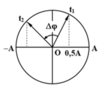
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)
tại t_2 ta có
W_đ/W_t = 1 --> x=A/\eqrt{2}
W_đ = W_t -->W= 2 W_đ =0.128
tại t=0 W_t = W-W_đ =0.032 -->W_đ /W_t =3 hay x =+-A/2
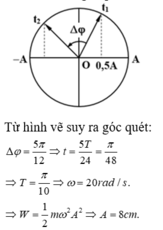
w= 20 rad/s W=1/2w^2*m*A^2 --->A=8
t/12+T/8 =5T/24=\pi/48 -->T=0.1\pi