Một vật nhỏ dao động điều hòa theo phương trình \(x=A\cos4\pi t\) (t tính bằng s). Tính từ t=0, khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nử độ lớn gia tốc cực đại là
A.0,083s.
B.0,125s.
C.0,104s.
D.0,167s.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 8 2015
Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s
VT
6 tháng 12 2018
Đáp án A
Chu kì dao động của vật 
= 0,5s.
Gia tốc có độ lớn bằng một nửa độ lớn gia tốc cực đại: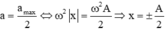 
Ta thấy rằng, tính từ t =0, khoảng thời gian ngắn nhất để gia tốc của vật có độ lớn bằng một nửa độ lớn gia tốc cực đại là t = T/6 = 0,083s
VT
24 tháng 9 2017
Đáp án D
Khi
theo chiều dương.
Thời gian nhỏ nhất ứng với vật đi từ t = 0 (tại biên dương) đến theo chiều dương và quay được góc αmin = 7π/6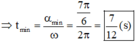 
VT
11 tháng 8 2017
Đáp án D
Tốc độ bằng một nửa tốc độ cực dại có li độ tương ứng x = 3 2 A
→ Thời gian ngắn nhất vật đi từ x = 0 đến x = 3 2 A là ∆ t = T 6
VT
2 tháng 1 2017
Chọn đáp án D
Tốc độ bằng một nửa tốc độ cực dại có li độ tương ứng: x = 3 2 A
→ Thời gian ngắn nhất vật đi từ x = 0 đến x = 3 2 A là: Δ t = T 6
Chu kì: T = 0,5s
Độ lớn của gia tốc: \(|a| = \omega^2|x|\) nên khi khi \(|a| = \frac{a_{max}}{2}\) thì \(x = \pm\frac{A}{2}\)
Biểu diễn bằng véc tơ quay ta có:
Ban đầu véc tơ quay xuất phát tại M, thời điểm gần nhất thỏa mãn điều kiện, véc tơ quay đến N, góc quay 600
Thời gian: \(t = \frac{60}{360}T = \frac{T}{6}\)=0,5/6 = 0,083s
c