đoạn mạch AB gồm cuộn dây thuần cam L, điện trở R, và tụ điện C mắc nối tiếp. đặt điện áp u= U căn 2 cos (wt +pi/2) V ( w thay đổi được và U khong đổi) vào hai đầu đoạn mạch . biết 2L>CR^2 . khi w=120pi (rad/s) . điện áp hiệu dụng hai đầu cuộn dây đạt cực đại và bằng 120V. khi w=100pi (rad/s), công suất của toàn mạch đạt giá trị cực đại . giá trị U gần giá trị nào nhất
A.80V B.85V C.90V D.100V

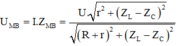
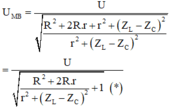
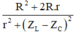
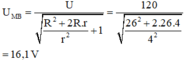
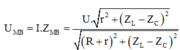
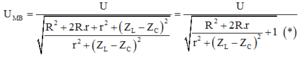
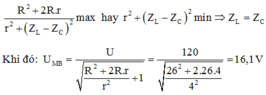
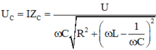
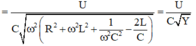
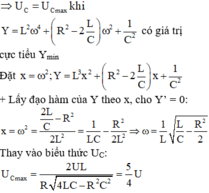

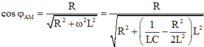
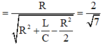

\(\omega\)thay đổi để \(U_{Lmax}\) thì
\(\omega=\frac{1}{C}.\frac{1}{\sqrt{\frac{L}{C}-\frac{R^2}{2}}}=120\pi\)\(\Rightarrow\frac{1}{\sqrt{LC-\frac{R^2C^2}{2}}}=120\pi\)(1)
\(U_{Lmax}=\frac{2UL}{R\sqrt{4LC-R^2C^2}}=120\)(2)
\(\omega\)thay đổi để P max thì:
\(\frac{1}{\sqrt{LC}}=100\pi\)(3)
Từ (3) \(\Rightarrow LC=\frac{1}{10^4\pi^2}\) (4), thay vào (1) \(\Rightarrow RC=\frac{\sqrt{22}}{600\pi}\)(5)
Lấy (4) : (5) \(\Rightarrow\frac{L}{R}=\frac{3}{50\sqrt{22}\pi}\)
Thay tất cả vào (2) \(\Rightarrow2U.\frac{3}{50\sqrt{22}\pi}.\frac{1}{\sqrt{4.\frac{1}{10^4\pi^2}-\frac{22}{600^2\pi^2}}}=120\Rightarrow U=86V\)
Đáp án B là gần nhất.