Mng giúp mik nhaaaa




Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


IX
2. j
3. i
4. f
5. c
6. a
7. h
8. e
9. g
10. d
XI
2. part => parts
3. a => an
4. a => an
5. a => the
6. are => will be (không chắc lắm)
7. taking => take
8. are => is
C.
Bài 1
1. C
2. B
3. C
4. B
(Nên double-check trước khi chép)

(2\(x\) + 7) ⋮ (\(x\) + 1) (đk \(x\) ≠ -1; \(x\in\)Z)
2\(x\) + 2 + 5 ⋮ \(x\) + 1
2.(\(x\) + 1) + 5 ⋮ \(x\) + 1
5 ⋮ \(x\) + 1
\(x\) + 1 \(\in\) Ư(5) = {-5; -1; 1; 5}
\(x\) \(\in\) {-6; -2; 0; 4}

2:
a: Xét tứ giác DIHK có
\(\widehat{DIH}=\widehat{DKH}=\widehat{IDK}=90^0\)
Do đó: DIHK là hình chữ nhật
Suy ra: DH=KI(1)
Xét ΔDEF vuông tại D có DH là đường cao ứng với cạnh huyền EF
nên \(DH^2=HE\cdot HF\left(2\right)\)
Từ (1) và (2) suy ra \(IK^2=HE\cdot HF\)



a, Theo tc 2 tt cắt nhau: \(AE=EC;BF=CF\)
Vậy \(AE+BF=EC+CF=EF\)
b, Vì \(\left\{{}\begin{matrix}AE=EC\\\widehat{EAO}=\widehat{ECO}=90^0\\OE.chung\end{matrix}\right.\) nên \(\Delta AOE=\Delta COE\)
\(\Rightarrow\widehat{AOE}=\widehat{EOC}\) hay OE là p/g \(\widehat{AOC}\)
Cmtt: \(\Delta BOF=\Delta COF\Rightarrow\widehat{BOF}=\widehat{COF}\) hay OF là p/g \(\widehat{BOC}\)
Vậy \(\widehat{EOF}=\widehat{COF}+\widehat{COE}=\dfrac{1}{2}\left(\widehat{AOC}+\widehat{BOC}\right)=90^0\) hay OE⊥OF

1. a) mẹ
b) thân mẫu
2. a) phu nhân
b) vợ
3. a) chết, lâm chung
b) lâm chung
4. a) giáo huấn
b) dạy bảo

Ta có: \(\left(2n+3\right)⋮\left(2n+1\right)\)
\(\Rightarrow\left(2n+1+2\right)⋮\left(2n+1\right)\)
Vì \(\left(2n+1\right)⋮\left(2n+1\right)\) nên để \(\left(2n+1+2\right)⋮\left(2n+1\right)\) thì \(2⋮\left(2n+1\right)\)
\(\Rightarrow2n+1\inƯ\left(2\right)\)
\(\Rightarrow2n+1\in\left\{1;2;-1;-2\right\}\)
\(\Rightarrow2n\in\left\{0;1;-2;-3\right\}\)
\(\Rightarrow n\in\left\{0;\frac{1}{2};-1;-\frac{3}{2}\right\}\)
\(2n+3⋮2n+1\)
\(2n+3=2n+1+2⋮2n+1\)
mà \(2n+1⋮2n+1\)
\(\Rightarrow2⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(2\right)\left\{1;2\right\}\)
| 2n + 1 | 1 | 2 |
| 2n + 1 | 0 | \(n\notinℕ\) |
Vậy \(n=0\)
sai thì cho mk xl nha!!!

e: \(E=\dfrac{x^2-9-x^2+4-x^2+9}{\left(x+3\right)\left(x-2\right)}\)
\(=\dfrac{x+2}{x+3}\)
a: \(A=\dfrac{4x^2+x^2-2x+1+x^2+2x+1}{\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{6x^2+2}{\left(x-1\right)\left(x+1\right)}\)





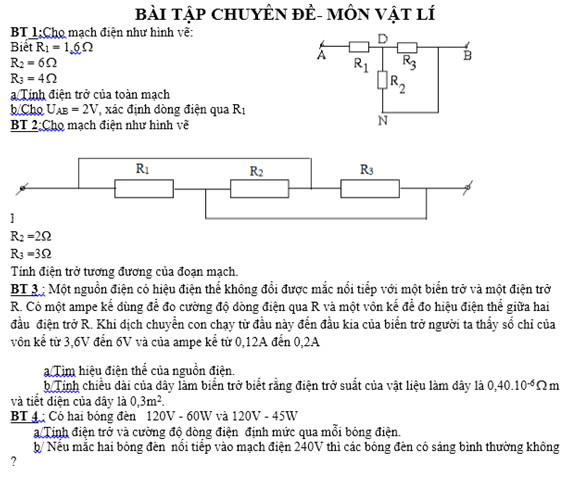 mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
mng giúp mik bài 1 vs bài 3 vs, mik cần gấp lắm, cảm ơn mng.
