tìm x,y thoả mãn x^2 12y^2-4xy 2x-28y 19 < hoặc = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DP
1
18 tháng 4 2023
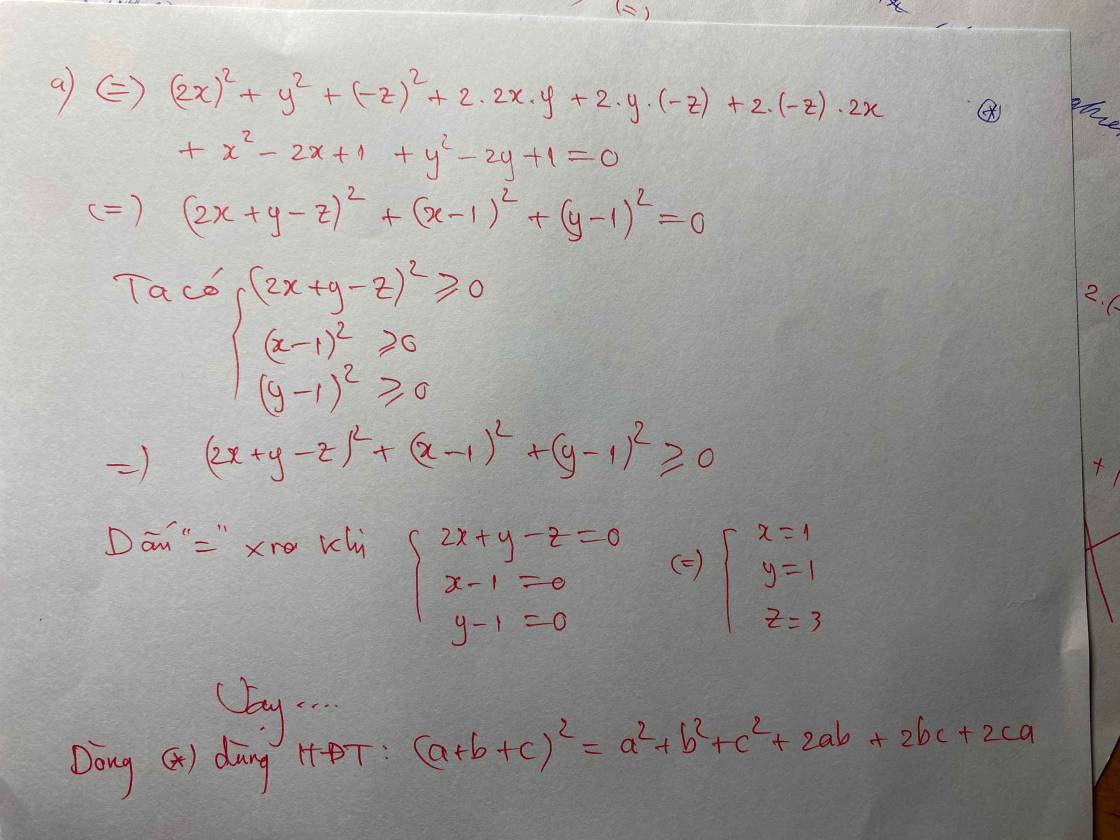
Học tốt nha bn ! ( dòng * ko cần ghi vào đâu bn đây là nháp giở của mik )
HP
0
6 tháng 6 2016
\(x^2+4y^2+z^2=2x+12y-4z-14\)
\(\Rightarrow x^2+4y^2+z^2-2x-12y+4z+14=0\)
\(\Rightarrow\left(x^2-2x+1\right)+\left(4y^2-12y+9\right)+\left(z^2+4z+4\right)=0\)
\(\Rightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\)
Ta có : \(\left(x-1\right)^2\ge0\Rightarrow x-1=0\Rightarrow x=1\)
\(\left(2y-3\right)^2\ge0\Rightarrow2y-3=0\Rightarrow2y=3\Rightarrow y=\frac{3}{2}\)
\(\left(z+2\right)^2\ge0\Rightarrow z+2=0\Rightarrow z=-2\)
24 tháng 5 2021
`P=1/(x^2+y^2)+1/(xy)+4xy`
`=1/(x^2+y^2)+1/(2xy)+4xy+1/(4xy)+1/(4xy)`
Áp dụng bunhia dạng phân thức
`=>1/(x^2+y^2)+1/(2xy)>=4/(x+y)^2`
Mà `(x+y)^2<=1`
`=>1/(x^2+y^2)+1/(2xy)>=4`
Áp dụng cosi:
`4xy+1/(4xy)>=2`
`4xy<=(x+y)^2<=1`
`=>1/(4xy)>=1`
`=>P>=4+2+1=7`
Dấu "=" `<=>x=y=1/2`
TQ
4
7 tháng 5 2016
\(=\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\)
\(\Rightarrow x=1;y=\frac{3}{2};z=-2\)
7 tháng 5 2016
Ta có:
x2+4y2+z2-2x-12y-4z-14=0
x2-2x+1+z2-4z+4+4y2-12y+9=0
(x-1)2+(z-2)2+(2y-3)2=0
Tổng 3 số không âm bằng 0
<=> x-1=0 và z-2=0 và 2y-3=0
<=> x=1 và z=2 và y=3/2
BM
1
20 tháng 9 2019
\(x^2-4xy+4y^2+y^2+2xy+1-4\)
\(\left(x-2y\right)^2+\left(y+1\right)^2-4\) > -4
Dấu = xảy ra khi \(\hept{\begin{cases}x-2y=0\\y+1=0\end{cases}< =>\hept{\begin{cases}x=-2\\y=-1\end{cases}}}\)
NV
0
Ta có:
\(x^2+12y^2-4xy+2x-28y+19\)
\(=x^2+4y^2+1-4xy+2x-4y+8y^2-24y+18\)
\(=\left(x-2y+1\right)^2+2\left(2y-3\right)^2\le0\)
\(\Leftrightarrow\hept{\begin{cases}x-2y+1=0\\2y-3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=\frac{3}{2}\end{cases}}\)