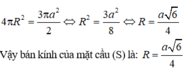Giai giúp em với ạ : Cho hình vuông ABCD có AB=5.Gọi MN lầ lượt là trung điểm của AB,AC
a,tính diện tích mcn
b.tính sin góc mcn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: \(NM=\dfrac{BC}{2}=3.5\left(cm\right)\)

a, \(BC=BH+CH=10\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AB=\sqrt{BH\cdot BC}=6\left(cm\right)\\AC=\sqrt{CH\cdot BC}=8\left(cm\right)\end{matrix}\right.\)
\(\sin B=\dfrac{AC}{BC}=\dfrac{4}{5}\approx\sin53^0\Rightarrow\widehat{B}\approx53^0\\ \Rightarrow\widehat{C}\approx90^0-53^0=37^0\)
b, Vì \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\) nên AMHN là hcn
Do đó \(MN=AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
Áp dụng HTL: \(AM\cdot MB=HM^2;AN\cdot NC=HN^2\)
Áp dụng PTG: \(HM^2+HN^2=MN^2=AH^2\)
Vậy \(AM\cdot MB+AN\cdot NC=AH^2\)

Chọn C
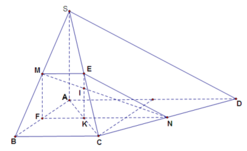
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và 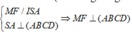
hay tứ giác MENF là hình thang vuông tại M, F
![]()
![]()
Ta có: 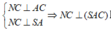 hay E là hình chiếu vuông góc của N lên (SAC)
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì ![]()
![]()
![]()
![]()

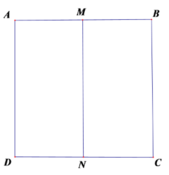
Mặt trụ tạo bởi hình vuông ABCD khi quay quanh MN có đường cao h = a và bán kính đáy ![]()
Diện tích 1 đáy và diện tích xung quanh của hình trụ là:
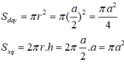
Nên có diện tích toàn phần của hình trụ:
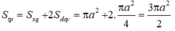
Mặt cầu (S) có bán kính R có diện tích bằng Stp của mặt trụ nên: