Một công ti dự định cho công nhân đi Suối Tiên nhưng chỉ có một xe mà một xe chỉ có thể cho 7 người mà có 67 công nhân .Hỏi phải thuê bao nhiêu chiếc xe nữa mới đủ chỗ ngồi và dư mấy chỗ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
18 tháng 11 2023
Gọi số xe loại 25 chỗ ngồi mà trường thuê là \(x\left(x\in N,12>x>0\right)\)
Số xe loại 45 chỗ ngồi mà trường thuê là \(y\left(y\in N,12>y>0\right)\)
Ta có: \(x+y=12\left(1\right)\)
Do chỉ có hai xe vừa đủ chỗ ngồi các xe còn lại đều thừa 1 chỗ
Số xe bị thừa chỗ là:
\(12-2=10\) (xe) ⇒ dư 10 chỗ
Vậy tổng số chỗ ngồi 12 xe này là: `450 + 10 = 460` (chỗ)
⇒ \(25x+45y=460\left(2\right)\)
Từ (1) và (2) ta có hệ pt:
\(\left\{{}\begin{matrix}x+y=12\\25x+45y=460\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}25x+25y=300\\25x+45y=460\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}20y=160\\x+y=12\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=8\left(tm\right)\\x=12-8\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y=8\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
Vậy số xe 25 chỗ trường thuê là 4 xe, số xe 45 chỗ mà trường thuê là 8 xe
CM
15 tháng 1 2019
Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
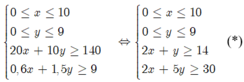
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.
CM
29 tháng 3 2017
Gọi x là số xe 12 chỗ và y là số xe 7 chỗ ngồi (x, y ∈ N*).
Số học sinh đi xe loại 12 chỗ là: 12x
Số học sinh đi xe loại 7 chỗ là: 7y
Theo đề bài ta có: 12x + 7y = 64 (*)
Ta có: 12x ⋮ 4, 64 ⋮ 4 nên 7y ⋮ 4
Vì ƯCLN(7,4) = 1 nên y ⋮ 4
Từ (*) suy ra: 7y < 64 => y ≤ 9
Mà y ⋮ 4 nên y ∈ {4;8}
+ Nếu y = 4 thì thay vào (*) ta được: 12x + 7.4 = 64 => x = 3 (thỏa mãn)
+ Nếu y = 8 thì thay vào (*) ta được: 12x + 7.8 = 64 => x = 8:12 (loại)
Vậy, có 3 xe 12 chỗ ngồi và 4 xe 7 chỗ ngồi
23 tháng 4 2021
Gọi x là số xe 12 chỗ và y là số xe 7 chỗ ngồi (x, y ∈ N*).
Số học sinh đi xe loại 12 chỗ là: 12x
Số học sinh đi xe loại 7 chỗ là: 7y
Theo đề bài ta có: 12x + 7y = 64 (*)
Ta có: 12x ⋮ 4, 64 ⋮ 4 nên 7y ⋮ 4
Vì ƯCLN(7,4) = 1 nên y ⋮ 4
Từ (*) suy ra: 7y < 64 => y ≤ 9
Mà y ⋮ 4 nên y ∈ {4;8}
+ Nếu y = 4 thì thay vào (*) ta được: 12x + 7.4 = 64 => x = 3 (thỏa mãn)
+ Nếu y = 8 thì thay vào (*) ta được: 12x + 7.8 = 64 => x = 8:12 (loại)
Vậy, có 3 xe 12 chỗ ngồi và 4 xe 7 chỗ ngồi
10 tháng 4
Gọi x là số xe 12 chỗ và y là số xe 7 chỗ ngồi (x, y ∈ N*).
Số học sinh đi xe loại 12 chỗ là: 12x
Số học sinh đi xe loại 7 chỗ là: 7y
Theo đề bài ta có: 12x + 7y = 64 (*)
Ta có: 12x ⋮ 4, 64 ⋮ 4 nên 7y ⋮ 4
Vì ƯCLN(7,4) = 1 nên y ⋮ 4
Từ (*) suy ra: 7y < 64 => y ≤ 9
Mà y ⋮ 4 nên y ∈ {4;8}
+ Nếu y = 4 thì thay vào (*) ta được: 12x + 7.4 = 64 => x = 3 (thỏa mãn)
+ Nếu y = 8 thì thay vào (*) ta được: 12x + 7.8 = 64 => x = 8:12 (loại)
Vậy, có 3 xe 12 chỗ ngồi và 4 xe 7 chỗ ngồi
21 tháng 3 2016
Xí nghiệp thuê số xe là:
12 : 3 = 4 (xe)
Trên thực tế mỗi xe chở được số người là:
172 : 4 = 43 (người)
Đáp số: 43 người
28 tháng 6 2021
- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :
can thue so xe la:
67:7=9(du 4 nguoi)
ds:9(du4)