Chứng minh \(\forall\) n \(\in\) N, n > 1 ta có \(\dfrac{1}{n-1}-\dfrac{1}{n}>\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TC
Trên con đường thành công không có....
25 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
18 tháng 12 2021
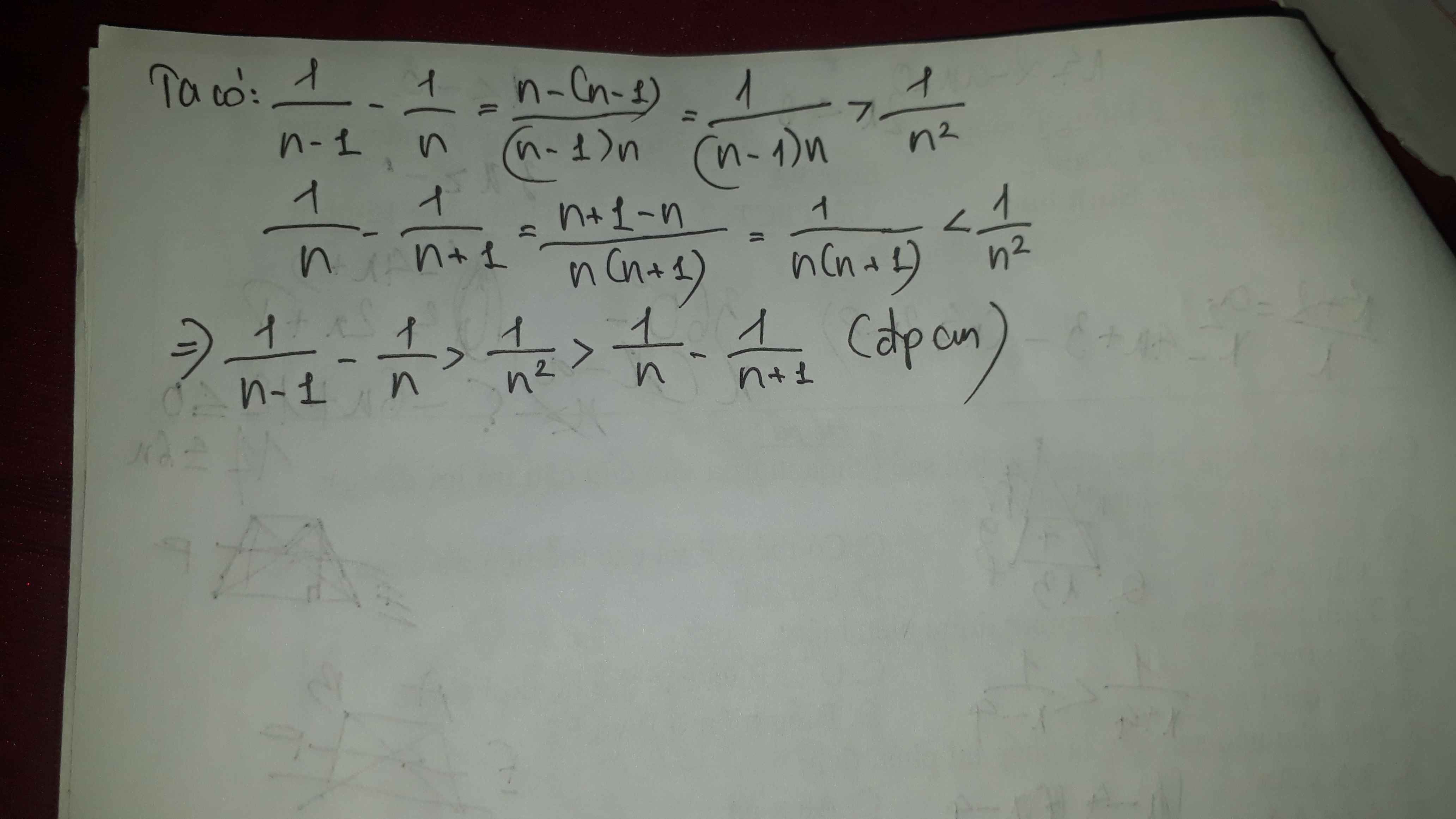
a: \(VT=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
19 tháng 12 2021
\(a,n=1\Leftrightarrow\dfrac{1}{1.2}=\dfrac{1}{2}\left(đúng\right)\\ G\text{/}s:n=k\Leftrightarrow\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{k\left(k+1\right)}=\dfrac{k}{k+1}\\ \text{Với }n=k+1\\ \text{Cần cm: }\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{k\left(k+1\right)}+\dfrac{1}{\left(k+1\right)\left(k+2\right)}=\dfrac{k+1}{k+2}\\ \text{Ta có }VT=\dfrac{k}{k+1}+\dfrac{1}{\left(k+1\right)\left(k+2\right)}=\dfrac{k^2+2k+1}{\left(k+1\right)\left(k+2\right)}\\ =\dfrac{\left(k+1\right)^2}{\left(k+1\right)\left(k+2\right)}=\dfrac{k+1}{k+2}=VP\)
Vậy với \(n=k+1\) thì mệnh đề cũng đúng
Vậy theo pp quy nạp ta đc đpcm
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Ta có: \(n\left(n-1\right)=n^2-n< n^2\Rightarrow\dfrac{1}{n\left(n-1\right)}>\dfrac{1}{n^2}\)
\(n\left(n+1\right)=n^2+n>n^2\Rightarrow\dfrac{1}{n\left(n+1\right)}< \dfrac{1}{n^2}\)
Từ đó:
\(\dfrac{1}{n-1}-\dfrac{1}{n}=\dfrac{n-\left(n-1\right)}{n\left(n-1\right)}=\dfrac{1}{n\left(n-1\right)}>\dfrac{1}{n^2}\) (1)
\(\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{1}{n\left(n+1\right)}< \dfrac{1}{n^2}\) (2)
(1);(2) \(\Rightarrow\dfrac{1}{n-1}-\dfrac{1}{n}>\dfrac{1}{n^2}>\dfrac{1}{n}-\dfrac{1}{n+1}\) (đpcm)
AH
Akai Haruma
Giáo viên
7 tháng 9 2018
Bạn xem lời giải tại đây:
Câu hỏi của Lệ Nguyễn Thị Mỹ - Toán lớp 9 | Học trực tuyến