K
Khách
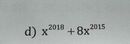
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
V
8 tháng 5 2019
๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉๖²⁴ʱƒɾëë༉ 甘道夫工程采用激光女可靠
H1
21 tháng 4 2021
a)ta có \(\Delta=b^2-4ac\)=1\(^2\)-4*1*1=-3
=>phương trình vô nghiệm vì \(\Delta< 0\)
b)ta có x\(^2\)+x+1=x\(^2\)+2.x.\(\dfrac{1}{2}\)+\(\dfrac{1}{4}\)+1-\(\dfrac{1}{4}\)=\(\left(x+\dfrac{1}{2}\right)^2\)+\(\dfrac{3}{4}\)
vì \(\left(x+\dfrac{1}{2}\right)^2\)>0 \(\forall x\in R\)
\(\left(x+\dfrac{1}{2}\right)^2\)+\(\dfrac{3}{4}\)>\(\dfrac{3}{4}\)\(\forall x\in R\)
=>GTNN =3/4 khi và chỉ khi \(\left(x+\dfrac{1}{2}\right)^2=0\)<=>x=-\(\dfrac{1}{2}\)
8 tháng 5 2021
`x^2-x+1/4=0`
`<=>x^2-1/2x-1/2x+1/4=0`
`<=>x(x-1/2)-1/2(x-1/2)=0`
`<=>(x-1/2)^2=0`
`<=>x=1/2`
Vậy nghiệm là `1/2`
28 tháng 7 2017
a) Để đa thức f(x) có nghiệm là 1 và 3 thì \(1^3-a.1^2-9.1+b=3^3-a.3^2-9.3+b=0\)
=> \(1-a-9+b=27-9a-27+b\)
=> \(-a+9a+b-b=8\Rightarrow8a=8\Rightarrow a=1\)
Từ đó tính được b = 9.
b) Thay kết quả câu a vào f(x) ta được f(x) = \(x^3-x^2-9x+9\)
Đa thức f(x) có nghiệm khi:
\(x^3-x^2-9x+9=x^2\left(x-1\right)-9\left(x-1\right)\)
\(=\left(x^2-9\right)\left(x-1\right)=0\Rightarrow\orbr{\begin{cases}x^2-9=0\\x-1=0\end{cases}}\)
Từ đó tìm được tập nghiệm của f(x) là {-3;1;3}.
12 tháng 8 2015
Vì Q(x) có một nghiệm là - 3 nên thay x = 3 ta có :
Q(-3) = (-3)^2 - 3 .m - 12 = 0
= 9 - 3m - 12 = 0
=>- 3m - 3 = 0
=> -3m = 3
=> m = -1
Thay m = -1 ta có Q(x ) = x^2 -x - 12
Q(x) = 0 => x^2 - x - 12 = 0 => x^2 - 4x + 3x - 12 = 0
=> x(x-4) + 3 (x-4 ) = 0
=> ( x+ 3 )(x- 4 ) = 0
=> x + 3 = 0 hoặc x - 4 = .0
=> x= -3 hoặc x = 4
19 tháng 4 2020
Trả lời:
A= 2X^2-x
Đa thức A(x) có nghiệm khi: x 2 − 2 x = 0 x2−2x=0 → x ( x − 2 ) = 0 →x(x−2)=0
→ [ x = 0 x − 2 = 0 ⇒ x = 2 →[x=0x−2=0⇒x=2
Vậy x = 0, x = 2 là nghiệm của đa thức A(x)
~Học tốt!~
16 tháng 4 2019
a) vì y=2 là một nghiện của đt
=> thay y=2 vào đt
t/có: f(2)=2^2-9.2+a=0
=>4-18+a=0
=>a=1
29 tháng 4 2015
1) Ta có: 2x2 + 2x + 1 = 0
<=> x2 + (x2 + 2x + 1) = 0
<=> x2 + (x+ 1)2 = 0 <=> x = x+ 1 = 0 (Vì x2 \(\ge\) 0 và (x+ 1)2 \(\ge\) 0 với mọi x)
x = x+ 1 => 0 = 1 Vô lý
Vậy đa thức đã cho ko có nghiệm
2) a) x3-2x2-5x+6 = 0
=> x3 - x2 - x2 + x - 6x + 6 = 0
=> ( x3 - x2) - (x2 - x) - (6x - 6) = 0 => x2.(x- 1) - x(x - 1) - 6(x - 1) = 0
=> (x - 1).(x2 - x - 6) = 0 => (x -1).(x2 - 3x + 2x - 6) = 0
=> (x- 1).[x(x - 3) + 2.(x - 3)] = 0 => (x - 1).(x + 2).(x - 3) = 0
=> x- 1= 0 hoặc x + 2 = 0 hoặc x - 3 = 0
=> x = 1 hoặc x = -2 hoặc x = 3
Đa thức đã cho có 3 nghiệm là: 1; -2 ; 3
b) x3 + 3x2 - 6x - 8 = 0
=> x3 + x2 + 2x2 + 2x - 8x - 8 = 0
=> x2.(x + 1) + 2x.(x + 1) - 8 (x + 1) = 0
=> (x+ 1). [x2 + 2x - 8] = 0
=> (x+1).[x2 + 4x - 2x - 8] = 0 => (x +1).[x.(x+4) - 2.(x+4)] = 0
=> (x +1). (x -2). (x+4) = 0
=> x+ 1 hoặc x - 2 = 0 hoặc x+ 4 = 0
=> x = -1 hoặc x = 2 hoặc x = -4
Đa thức đã cho có 3 nghiệm là -1; 2; -4
12 tháng 5 2019
Để 4x^2 + 7x + 6 có nghiệm ta có:
4x^2 + 7x + 6 = 0
4x . x + 7x = -6
11x . x = -6
x^2 = \(\frac{-6}{11}\)
Vậy x = - \(\sqrt{\frac{6}{11}}\)là nghiệm của đa thức trên
Ta có : x2018 + 8x2015 = 0
<=> x2015(x3 + 8) = 0
<=> \(\orbr{\begin{cases}x^{2015}=0\\x^3+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^3=\left(-2\right)^3\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-2\end{cases}}\)
Vậy \(x\in\left\{0;-2\right\}\)là nghiệm đa thức trên