Cho tam giác ABC nội tiếp (O), đường cao AD, BE, CF, trực tâm H. AH cắt (O) tại K. Chứng minh: DH=DK.
MỌI NGƯỜI ƠI GIÚP EM VỚI EM CÀN GẤP Ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
25 tháng 7 2021
Lời giải:
$\widehat{HBD}=\widehat{EBC}=\widehat{CAD}$ (cùng phụ góc $\widehat{ACB}$)
$\widehat{CAD}=\widehat{CAK}=\widehat{KBC}=\widehat{KBD}$ (góc nt chắn cung $CK$)
$\Rightarrow \widehat{HBD}=\widehat{KBD}$
Xét tam giác vuông tại $D$ là $HBD$ và $KBD$ có:
$\widehat{HBD}=\widehat{KBD}$ (cmt)
$BD$ chung
$\Rightarrow \triangle HBD=\triangle KBD$ (g.c.g)
$\Rightarrow HD=KD$ (đpcm)
31 tháng 1 2023
a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC
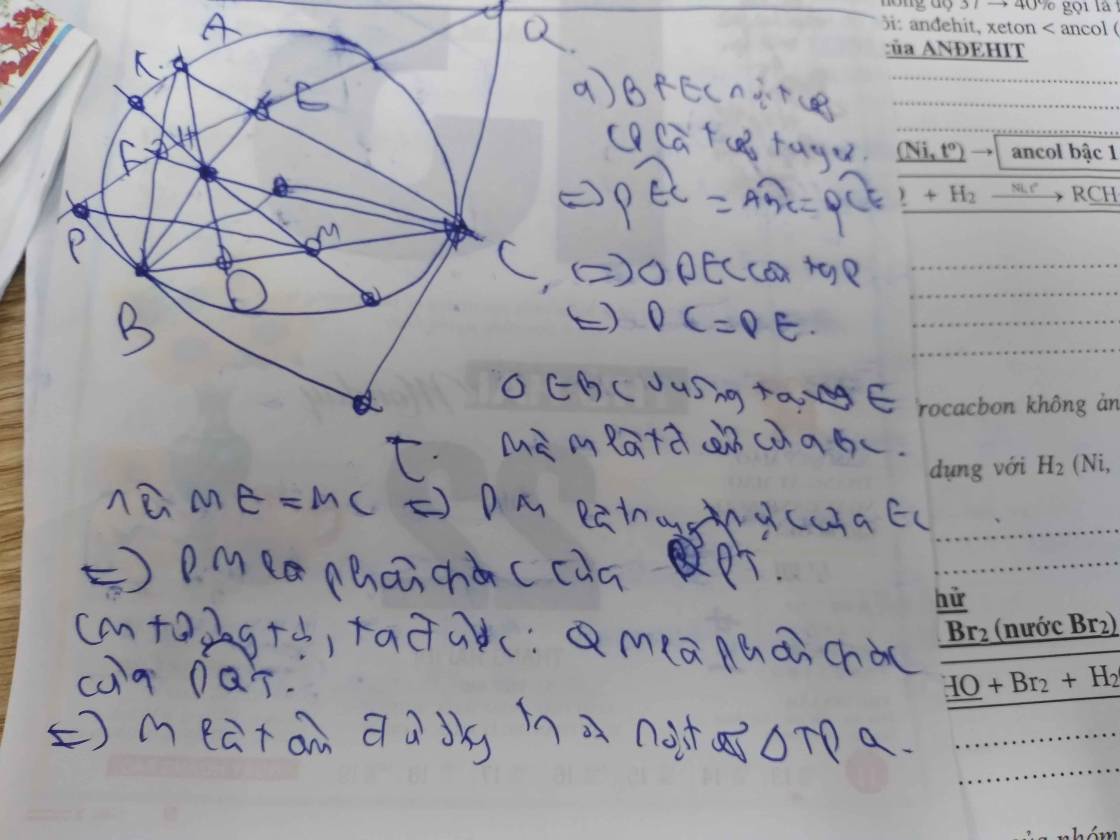
Xét đường tròn (O) có
sđ\(\widehat{BCK}=\)sđ\(\widehat{BAK}\) (Góc nội tiếp đường tròn cùng chắn cung BK) (1)
Xét tứ giác BFEC có F; E cùng nhìn BC dưới 1 góc vuông => E; F cùng nằm trên đường tròn đường kính BC
=> sđ\(\widehat{BCF}=\)sđ\(\widehat{FEB}\) (Góc nội tiếp đường tròn cùng chắn cung BF) (2)
Xét tứ giác AFHE có E và F cùng nhìn AH dưới 1 góc vuông => E; F cùng nằm trên đường tròn đường kính AH
=> sđ\(\widehat{BAK}=\)sđ\(\widehat{FEB}\) (Góc nội tiếp đường tròn cùng chắn cung HF) (3)
Từ (1) (2) và (3) \(\Rightarrow\widehat{BCF}=\widehat{BCK}\) => BC là phân giác của \(\widehat{KCH}\)
Ta có \(BC\perp KH\)
=> \(\Delta KCH\) cân tại C (Tam giác có đường phân giác đồng thời là đường cao thì tg đó là tg cân)
\(\Rightarrow DH=DK\) (Trong tg cân đường cao đồng thời là đường trung tuyến)