Hộ từ bài 3 đến hết ạ, làm được đến đâu thì làm, mình cảm ơn trước
Hộ từ bài 3 đến hết ạ, làm được đến đâu thì làm, mình cảm ơn trước
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


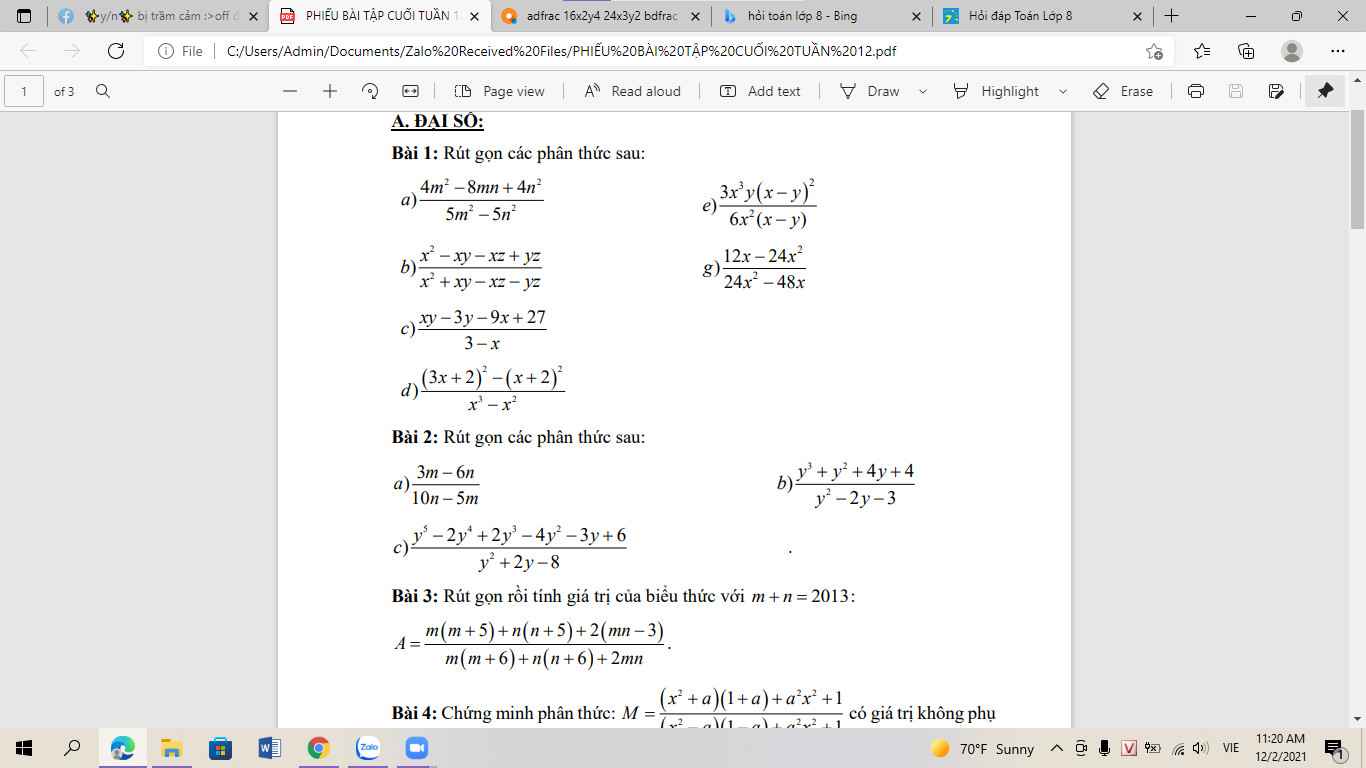
Bài 1:
a) \(=\dfrac{\left(2m-2n\right)^2}{5\left(m^2-n^2\right)}=\dfrac{4\left(m-n\right)^2}{5\left(m-n\right)\left(m+n\right)}=\dfrac{4m-4n}{4m+5n}\)
b) \(=\dfrac{\left(x-y\right)\left(x-z\right)}{\left(x+y\right)\left(x-z\right)}=\dfrac{x-y}{x+y}\)
c) \(=\dfrac{\left(x-3\right)\left(y-9\right)}{-\left(x-3\right)}=9-y\)
d) \(=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}=\dfrac{8x\left(x+1\right)}{x^2\left(x-1\right)}=\dfrac{8x+8}{x^2-x}\)
e) \(=\dfrac{xy\left(x-y\right)}{2}=\dfrac{x^2y-xy^2}{2}\)
g) \(=\dfrac{12x\left(1-2x\right)}{24x\left(x-2\right)}=\dfrac{1-2x}{2x-4}\)
Bài 2:
a) \(=\dfrac{3\left(m-2n\right)}{-5\left(m-2n\right)}=-\dfrac{3}{5}\)
b) \(=\dfrac{\left(y+1\right)\left(y^2+4\right)}{\left(y-3\right)\left(y+1\right)}=\dfrac{y^2+4}{y-3}\)
c) \(=\dfrac{y^4\left(y-2\right)+2y^2\left(y-2\right)-3\left(y-2\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{\left(y-2\right)\left(y^4+2y^2-3\right)}{\left(y-2\right)\left(y+4\right)}=\dfrac{y^4+2y^2-3}{y+4}\)
Bài 3:
\(A=\dfrac{\left(m^2+2mn+n^2\right)+5\left(m+n\right)-6}{\left(m^2+2mn+n^2\right)+6\left(m+n\right)}=\dfrac{\left(m+n\right)^2+5\left(m+n\right)-6}{\left(m+n\right)^2+6\left(m+n\right)}=\dfrac{2013^2+5.2013-6}{2013^2+6.2013}=\dfrac{2012}{2013}\)

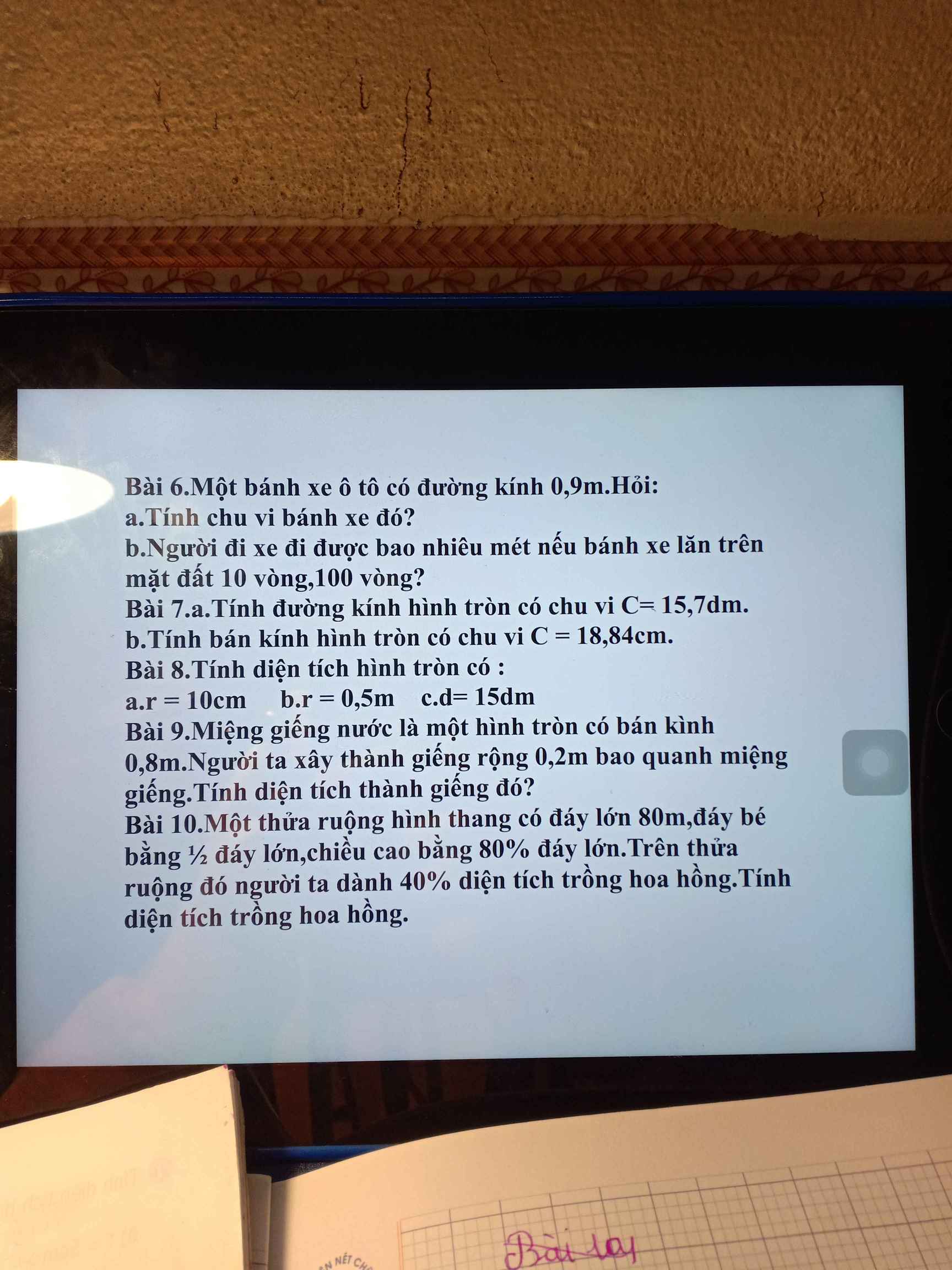
Tự làm,bài tập về nhà không tự suy nghĩ lại đăng lên để người khác làm hộ à.Học phải có tư duy.

11 c)
\(a^2+2\ge2\sqrt{a^2+1}\Leftrightarrow a^2+1-2\sqrt{a^2+1}+1\ge0\Leftrightarrow\left(\sqrt{a^2+1}-1\right)^2\ge0\) (luôn đúng)
12 a) Có a+b+c=1\(\Rightarrow\) (1-a)(1-b)(1-c)= (b+c)(a+c)(a+b) (*)
áp dụng BĐT cô-si: \(\left(b+c\right)\left(a+c\right)\left(a+b\right)\ge2\sqrt{bc}2\sqrt{ac}2\sqrt{ab}=8\sqrt{\left(abc\right)2}=8abc\) ( luôn đúng với mọi a,b,c ko âm )
b) áp dụng BĐT cô-si: \(c\left(a+b\right)\le\dfrac{\left(a+b+c\right)^2}{4}=\dfrac{1}{4}\)
Tương tự: \(a\left(b+c\right)\le\dfrac{1}{4};b\left(c+a\right)\le\dfrac{1}{4}\)
\(\Rightarrow abc\left(a+b\right)\left(b+c\right)\left(c+a\right)\le\dfrac{1}{4}\dfrac{1}{4}\dfrac{1}{4}=\dfrac{1}{64}\)

#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<p;
return 0;
}

1:
uses crt;
var a,b,c,max,min:longint;
begin
clrscr;
readln(a,b,c);
max=a;
if max<b then max:=b;
if max<c then max:=c;
min:=a;
if min>c then min:=c;
if min>b then min:=b;
writeln(max,' ',min);
readln;
end.