trong mặt phẳng có 6 điểm, trong đó không có ba điểm nào thẳng hàng. Hỏi
a) Vẽ được bao nhiêu đoạn thẳng đi qua các điểm đã cho?
b)Vẽ được bao nhiêu tam giác có ba đỉnh là ba điểm đã cho?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
E
8 tháng 3 2020
a, Vẽ được số đoạn thẳng đi qua các điểm đã cho là:
6 . ( 6 - 1 ) : 2 = 15 (đoạn thẳng)
b, Với mỗi đoạn thẳng , nối 2 đầu của đoạn thẳng này với 1 điểm khác ta được 1 tam giác.
Cố định 1 đoạn thẳng trong 15 đoạn thẳng , nối 2 đầu của đoạn thẳng này với 4 điểm còn lại ta được 4 tam giác . Có 15 đoạn thẳng như vậy nên có tất cả:
15 . 4 = 60 (tam giác)
Nhưng mỗi tam giác đã được tính ba lần nên số các tam giác tạo được từ 6 điểm này là:
60 : 3 = 20 (tam giác)
Đ/S
# HOK TỐT #
WW
26 tháng 6 2017
Lời giải:
a/ Cố định 1 điểm trong 6 điểm này, nối điểm này với 5 điểm còn lại ta được 5 đoạn thẳng.
Có 6 điểm như vậy nên có tất cả 6 . 5 = 30 (đoạn thẳng).
Nhưng mỗi đoạn thẳng đã được tính 2 lần nên số các đoạn thẳng tạo được từ 12 điểm này là 30 : 2 = 15 (đoạn thẳng).
b/
Với một đoạn thẳng, nối 2 đầu của đoạn thẳng này với 1 điểm khác ta được một tam giác.
Cố định 1 đoạn thẳng trong 15 đoạn thẳng, nối hai đầu của đoạn thẳng này với 4 điểm còn lại ta được 4 tam giác. Có 15 đoạn thẳng như vậy nên có tất cả 15 .4 = 60 (tam giác).
Nhưng mỗi tam giác đã được tính 3 lần nên số các tam giác tạo được từ 6 điểm này là 60 : 3 = 20 (tam giác).
Chúc bạn học tốt, thân!
CM
30 tháng 5 2018
Cứ chọn 3 điểm không thẳng hàng bất kì ta được một tam giác.
Việc lập các tam giác chính là chọn 3 điểm trong tập hợp 6 điểm đã cho và chính là tổ hợp chập 3 của 6.
Vậy có:
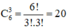cách lập.
16 tháng 7 2021
Sô tam giác vẽ đc là: (4.3.2):6= 4 tam giác
CM
25 tháng 3 2019
Đáp án là B
Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.
Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).
Như vậy, ta có C 6 3 = 20 tam giác.
NA
27 tháng 12 2018
a. Số đoạn thẳng vẽ được là : \(C^2_{16}=120\)
b. Số tam giác tạo thành là : \(C^3_{16}=560\)
15 hình
mk nghĩ là 15 hình đó bn